Question

（本小题满分9分）如图12，四边形ABCD是正方形，点E，K分别在BC，AB

上，点G在BA的延长线上，且CE=BK=AG.

⑴求证：①DE=DG；②DE⊥DG；

⑵尺规作图：以线段DE，DG为边作出正方形DEFG（要求：只保留作图痕迹，不写作法和证明）；

⑶连接⑵中的KF，猜想并写出四边形CEFK是怎样的特殊四边形，并证明你的猜想；

⑷当时，请直接写出的值.

 

Answer 1

解：⑴证明：∵ 四边形是正方形  ，∴，°.

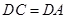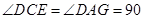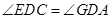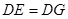又∵，∴⊿≌⊿.∴，.又∵,∴,∴.

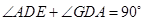⑵如图2（注：图3或其它画法正确的相应给分）

               

⑶四边形是平行四边形.

证明：设相交于点.

∵四边形和四边形都是正方形，∴AB∥CD,AB=CD, EF=DG, EF∥DG,

∵BK=AG, ∴KG=AB=CD, ∴四边形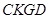为平行四边形. ∴CK=DG=EF, CK∥DG.

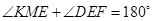∴.∴.∴CK∥EF,

∴四边形是平行四边形.

(注：由CK∥DG, EF∥DG得CK∥EF也可)

⑷.

解析:略