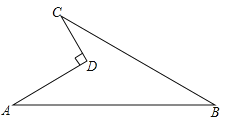
��Ŀ����
����Ŀ����ͼ������ABC�У�AB=AC��BD��AC��D��CE��AB��E��BD��CE�ཻ��F��
��֤��AFƽ����BAC��
���𰸡�֤��������.
������������������ȸ���AB=AC���ɵá�ABC=��ACB�����ɴ�ֱ���ɵ�90���Ľǣ�����BCE����BCD�У������ڽǺ�Ϊ180�����ɷֱ����BCE�͡�DBC�����õ�������������ȣ��ɵ�FB=FC������֤��ABF�ա�ACF���Ӷ�֤��AFƽ�֡�BAC��
���������֤������AB=AC(��֪)��
���ABC=��ACB(�ȱ߶ԵȽ�).
��BD��CE�ֱ��Ǹߣ�
��BD��AC,CE��AB(�ߵĶ���).
���CEB=��BDC=90��.
���ECB=90����ABC,��DBC=90����ACB.
���ECB=��DBC(��������).
��FB=FC(�ȽǶԵȱ�)��
����ABF����ACF��
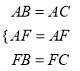 ��
��
����ABF����ACF(SSS)��
���BAF=��CAF(ȫ�������ζ�Ӧ�����)��
��AFƽ�֡�BAC.
�����͡������
��������
23
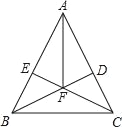
����Ŀ����ͼ������ABC�У�AC=BC����C=90����AD����ABC�Ľ�ƽ���ߣ�DE��AB������ΪE��
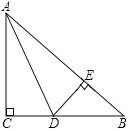
��1����֤��CD=BE��
��2����֪CD=2����AC�ij���
��3����֤��AB=AC+CD��
���𰸡���1�������������2��2+2![]() ����3���������.
����3���������.
�������������������1���ȸ��������жϳ���ABC�ǵ���ֱ�������Σ��ʡ�B=45��������DE��AB��֪��BDE�ǵ���ֱ�������Σ���DE=BE���ٸ��ݽ�ƽ���ߵ����ʼ��ɵó����ۣ�
��2���ɣ�1��֪����BDE�ǵ���ֱ�������Σ�DE=BE=CD���ٸ��ݹ��ɶ������BD�ij��������ɵó����ۣ�
��3���ȸ���HL�����ó�Rt��ACD��Rt��AED����AE=AC������CD=BE�ɵó����ۣ�
�����������1��������ABC��AC=BC����C=90����
����ABC�ǵ���ֱ�������Σ�
���B=45����
��DE��AB��
����BDE�ǵ���ֱ�������Σ�
��DE=BE��
��AD����ABC�Ľ�ƽ���ߣ�
��CD=DE��
��CD=BE��
��2�����ɣ�1��֪����BDE�ǵ���ֱ�������Σ�DE=BE=CD��
��DE=BE=CD=2��
��BD=![]() ��
��
��AC=BC=CD+BD=2+2![]() ��
��
��3����AD����ABC�Ľ�ƽ���ߣ�DE��AB��
��CD=DE��
��Rt��ACD��Rt��AED��
��![]() ��
��
��Rt��ACD��Rt��AED��
��AE=AC��
���ɣ�1��֪CD=BE��
��AB=AE+BE=AC+CD��

 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�