题目内容
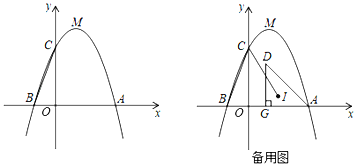
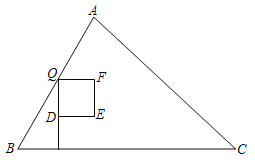
【题目】如图:在△ABC中,AB=5cm,BC=7cm,S△ABC=14cm2,点P从点B出发,以3cm∕s的速度沿边BC向终点C运动,过点P作PQ⊥BC交折线BAC于点Q,D为PQ中点,以DQ为边向右侧作正方形DEFQ.设正方形DEFQ与△ABC重叠部分图形的面积是y(cm2),点P的运动时间为x(s).
(1)∠C的度数为 ;
(2)当点P不与点C重合,且点F落在边AC上时x的值为 .
(3)当点P不与点B,C重合时,求y关于x的函数解析式;
(4)当直线BD平分△ABC的面积时,直接写出x的值.
【答案】(1)45°;(2)![]() ;(3)①0<x≤
;(3)①0<x≤![]() 时,y=4x2;②
时,y=4x2;②![]() <x≤1时,y=
<x≤1时,y=![]() ;;③1<x<
;;③1<x<![]() 时y=
时y=![]() ;(4)
;(4)![]()
【解析】
(1)作AM⊥BC于M,由三角形面积求出AM=4,由勾股定理得出BM=![]() =3,证出AM=CM,得出△ACM是等腰直角三角形,即可得出答案;
=3,证出AM=CM,得出△ACM是等腰直角三角形,即可得出答案;
(2)作AM⊥BC于M,则PQ∥AM,得出△BPQ∽△BMA,得出![]() =
=![]() =
=![]() ,求出PQ=4x,BQ=5x,得出QD=PD=2x,证明△AQF∽△ABC,得出
,求出PQ=4x,BQ=5x,得出QD=PD=2x,证明△AQF∽△ABC,得出![]() =
=![]() ,即可得出答案;
,即可得出答案;
(3)分三种情况:①0<x≤![]() 时,由正方形面积即可得出答案;
时,由正方形面积即可得出答案;
②![]() <x≤1时,延长FE交BC于N,则FN=PQ=4x,求出HN=CN=7﹣3x﹣2x=7﹣5x,GF=HF=9x﹣7,由正方形DEFQ的面积﹣△FGH的面积即可得出答案;
<x≤1时,延长FE交BC于N,则FN=PQ=4x,求出HN=CN=7﹣3x﹣2x=7﹣5x,GF=HF=9x﹣7,由正方形DEFQ的面积﹣△FGH的面积即可得出答案;
③1<x<![]() 时,延长FE交BC于N,点E在AC上,则FN=PQ=4x,求出QF=EF=EN=CN=
时,延长FE交BC于N,点E在AC上,则FN=PQ=4x,求出QF=EF=EN=CN=![]() (7﹣3x),由正方形面积即可得出答案;
(7﹣3x),由正方形面积即可得出答案;
(4)当直线BD平分△ABC的面积时,延长BD交AC于K,则K为AC的中点,△CPQ是等腰直角三角形,得出CP=PQ=7﹣3x,PD=![]() PQ=
PQ=![]() (7﹣3x),作KO⊥BC于O,则KO∥PQ,△OCK是等腰直角三角形,得出CO=KO=
(7﹣3x),作KO⊥BC于O,则KO∥PQ,△OCK是等腰直角三角形,得出CO=KO=![]() CK=2,△BPD∽△BOK,得出BO=BC﹣CO=5,
CK=2,△BPD∽△BOK,得出BO=BC﹣CO=5,![]() =
=![]() ,即可得出答案.
,即可得出答案.
解:(1)作AM⊥BC于M,如图1所示:
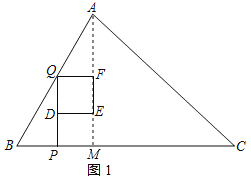
∵S△ABC=![]() BC×AM=
BC×AM=![]() ×7×AM=14,
×7×AM=14,
∴AM=4,
∴BM=![]() =
=![]() =3,
=3,
∴CM=BC﹣BM=7﹣3=4,
∴AM=CM,
∴△ACM是等腰直角三角形,
∴∠C=45°;
故答案为:45°;
(2)作AM⊥BC于M,如图2所示:

则PQ∥AM,
∴△BPQ∽△BMA,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
解得:PQ=4x,BQ=5x,
∵D为PQ中点,
∴QD=PD=2x,
∵四边形DEFQ是正方形,
∴QF=QD=2x,QF⊥PQ,
∵PQ⊥BC,
∴QF∥BC,
∴△AQF∽△ABC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=![]() ;
;
故答案为:![]() ;
;
(3)分三种情况:①0<x≤![]() 时,如图1所示:
时,如图1所示:
y=正方形DEFQ的面积=DQ2=4x2;
②![]() <x≤1时,如图3所示:
<x≤1时,如图3所示:
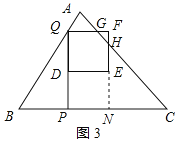
延长FE交BC于N,则FN=PQ=4x,△CNH、△FGH是等腰直角三角形,
∴HN=CN=7﹣3x﹣2x=7﹣5x,GF=HF=4x﹣(7﹣5x)=9x﹣7,
∴y=正方形DEFQ的面积﹣△FGH的面积=(2x)2﹣![]() ×(9x﹣7)2=
×(9x﹣7)2=![]() 2+63x﹣
2+63x﹣![]() ,
,
即y=![]() ;
;
③1<x<![]() 时,如图4所示:
时,如图4所示:
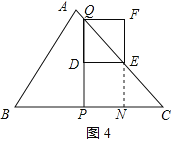
延长FE交BC于N,点E在AC上,则FN=PQ=4x,△CPQ、△CNE、△QFE是等腰直角三角形,
∴QF=EF=EN=CN=![]() (7﹣3x),
(7﹣3x),
∴y=![]() 正方形DEFQ的面积=
正方形DEFQ的面积=![]() [
[![]() (7﹣3x)]2=
(7﹣3x)]2=![]() 2﹣
2﹣![]() x+
x+![]() ,即y=
,即y=![]() ;
;
(4)当直线BD平分△ABC的面积时,连接BD并延长BD交AC于K,如图5所示:

则K为AC的中点,△CPQ是等腰直角三角形,
∴CP=PQ=7﹣3x,PD=![]() PQ=
PQ=![]() (7﹣3x),
(7﹣3x),
∵AC=![]() =4
=4![]() ,
,
∴CK=![]() AC=2
AC=2![]() ,
,
作KO⊥BC于O,
则KO∥PQ,△OCK是等腰直角三角形,
∴CO=KO=![]() CK=2,△BPD∽△BOK,
CK=2,△BPD∽△BOK,
∴BO=BC﹣CO=5,![]() =
=![]() ,即
,即![]() =
=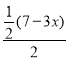 ,
,
解得:x=![]() .
.
即当直线BD平分△ABC的面积时,x的值为![]() .
.