题目内容
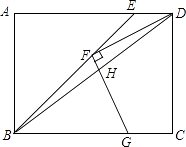
【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点G在边BC上，且∠GDF=∠ADF.连接EG，判断EG与DF的位置关系，并说明理由.
【答案】EG与DF的位置关系是EG⊥DF.
【解析】
先证明△ADE≌△BFE．，得到DE=EF，先证明△DGF是等腰三角形，再根据等腰三角形三线合一的性质得出结论．
EG与DF的位置关系是EG⊥DF．理由如下：
∵AD∥BC，∴∠ADE=∠BFE．
∵E是AB的中点，∴AE=BE．
又∵∠FEB=∠DEA，∴△ADE≌△BFE，∴DE=EF．
∵∠GDF=∠ADF，∠ADE=∠BFE，∴∠GDF=∠BFE，∴GD=GF．
∵DE=EF，∴EG⊥DF．
练习册系列答案
相关题目
【题目】在平面直角坐标系xOy中，⊙C的半径为r，P是与圆心C不重合的点，点P关于⊙C的限距点的定义如下：若P′为直线PC与⊙C的一个交点，满足r≤PP′≤2r，则称P′为点P关于⊙C的限距点，如图为点P及其关于⊙C的限距点P′的示意图． 
（1）当⊙O的半径为1时．
①分别判断点M（3，4），N（ 
，0），T（1， 
）关于⊙O的限距点是否存在？若存在，求其坐标；
②点D的坐标为（2，0），DE，DF分别切⊙O于点E，点F，点P在△DEF的边上．若点P关于⊙O的限距点P′存在，求点P′的横坐标的取值范围；
（2）保持（1）中D，E，F三点不变，点P在△DEF的边上沿E→F→D→E的方向运动，⊙C的圆心C的坐标为（1，0），半径为r，请从下面两个问题中任选一个作答．
问题1 | 问题2 |
若点P关于⊙C的限距点P′存在，且P′随点P的运动所形成的路径长为πr，则r的最小值为 | 若点P关于⊙C的限距点P′不存在，则r的取值范围为 |
