题目内容
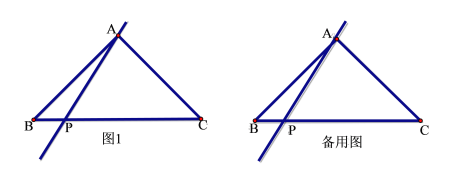
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,直线
,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于分别交于点
轴分别交于分别交于点![]() 、点
、点![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ,两直线交于点
,两直线交于点![]() ,且
,且![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)将直线![]() 向下平移一定的距离,使得平移后的直线经过
向下平移一定的距离,使得平移后的直线经过![]() 点,且与
点,且与![]() 轴交于点
轴交于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.

【答案】(1)![]() ;(2)32.
;(2)32.
【解析】
(1)将点E的坐标代入![]() 中,求出m,利用直线AB的解析式求出OB,根据
中,求出m,利用直线AB的解析式求出OB,根据![]() 得到OC的长,由此利用点E、C的坐标求得直线
得到OC的长,由此利用点E、C的坐标求得直线![]() 的解析式;
的解析式;
(2)根据![]() 求出点A的坐标,利用直线平移规律求得直线AF的解析式,得到点F的坐标,由直线CD求出点D的坐标,再连接OE,利用面积相加的关系得到四边形
求出点A的坐标,利用直线平移规律求得直线AF的解析式,得到点F的坐标,由直线CD求出点D的坐标,再连接OE,利用面积相加的关系得到四边形![]() 的面积.
的面积.
(1) 将点![]() 的坐标代入
的坐标代入![]() 中,得m=
中,得m=![]() ,
,
∴E(![]() ,
, ![]() ).
).
令![]() 中x=0,得y=5,
中x=0,得y=5,
∴B(0,5),
∴OB=5,
∵![]() ,
,
∴OC=4,即C(-4,0),
将E(![]() ,
, ![]() ),C(-4,0)代入
),C(-4,0)代入![]() 中,得
中,得
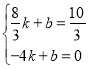 ,得
,得![]() ,
,
∴直线CD的解析式为![]() .
.
(2)令![]() 中y=0,得
中y=0,得![]() ,
,
解得x=8,∴A(8,0),
设直线![]() 向下平移后的解析式为
向下平移后的解析式为![]() ,将点A的坐标代入,得m=-4,
,将点A的坐标代入,得m=-4,
∴直线AF的解析式为![]() ,∴F(0,-4),
,∴F(0,-4),
∵直线CD的解析式为![]() ,
,
∴与y轴交点D(0,2),
连接OE,
∴四边形![]() 的面积=S△ODE+S△OAE+S△OAF,
的面积=S△ODE+S△OAE+S△OAF,
= ![]() ,
,
=32.


练习册系列答案
相关题目
【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A. 中位数是50 B. 众数是51 C. 方差是42 D. 极差是21