题目内容
【题目】三条边都相等的三角形叫做等边三角形,它的三个角都是60°.△ABC是等边三角形,点D在BC所在直线上运动,连接AD,在AD所在直线的右侧作∠DAE=60°,交△ABC的外角∠ACF的角平分线所在直线于点E.
(1)如图1,当点D在线段BC上时,请你猜想AD与AE的大小关系,并给出证明;
(2)如图2,当点D在线段BC的反向延长线上时,依据题意补全图形,请问上述结论还成立吗?请说明理由.
【答案】(1)AD=AE.理由见解析;(2)成立,理由见解析;
【解析】
(1)在AB上取一点M,使BM=BD,连接MD.则△BDM是等边三角形,则易证AM=DC,根据ASA即可证得△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得;
(2)延长BA到M,使AM=CD,与(1)相同,可证△BDM是等边三角形,然后证明△AMD≌△DCE(ASA),根据全等三角形的对应边相等,即可证得.
(1)结论:AD=AE.
理由:如图,在AB上取一点M,使BM=BD,连接MD.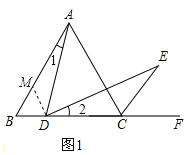
∵△ABC是等边三角形,
∴∠B=60°,BA=BC.
∴△BMD是等边三角形,∠BMD=60°.∠AMD=120°.
∵CE是外角∠ACF的平分线,
∴∠ECA=60°,∠DCE=120°.
∴∠AMD=∠DCE.
∵∠ADE=∠B=60°,∠ADC=∠2+∠ADE=∠1+∠B
∴∠1=∠2.
又∵BA-BM=BC-BD,即MA=CD.
在△AMD和△DCE中,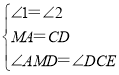 ,
,
∴△AMD≌△DCE(ASA).
∴AD=DE.
(2)正确.
证明:延长BA到M,使AM=CD,
与(1)相同,可证△BDM是等边三角形,
∵∠CDE=∠ADB+∠ADE=∠ADB+60°,
∠MAD=∠B+∠ADB=∠ADB+60°,
∴∠CDE=∠MAD,
同理可证,△AMD≌△DCE,
∴AD=DE.

【题目】抛物线![]() 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A. 1 B. 2 C. 3 D. 4






