题目内容
【题目】在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均数、众数和中位数:
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
【答案】
(1)解:观察表格,可知这组样本数据的平均数是 ![]() =
= ![]() =2,
=2,
∴这组样本数据的平均数为2,
∵这组样本数据中,3出现了17次,出现的次数最多,
∴这组数据的众数是3.
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,有 ![]() =2,
=2,
∴这组数据的中位数为2
(2)解:∵在50名学生中,读书多于2册的学生有18名,有300× ![]() =108.
=108.
∴根据样本数据,可以估计该校八年级300名学生在本次活动中读书多于2册的约有108名.
【解析】(1)由表格知这组样本数据的平均数是x=2,所以这组样本数据的平均数为2,因为这组样本数据中,3出现了17次,出现的次数最多,所以这组数据的众数是3,将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,所以这组数据的中位数为2;(2)在50名学生中,读书多于2册的学生有18名,可得300×(18÷50)=108.
【考点精析】认真审题,首先需要了解中位数、众数(中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数).

【题目】若一辆汽车以50 km/h的速度匀速行驶,行驶的路程为s(km),行驶的时间为t(h),则用t表示s的关系式为( )
A. s=50+50tB. s=50tC. s=50-50tD. 以上都不对
【题目】某校八年级全体男同学参加了跳绳比赛,从中随机抽取某班男同学的跳绳成绩,制作了如下频数分布表:
组别 | 99.5﹣109.5 | 109.5﹣119.5 | 119.5﹣129.5 | 129.5﹣139.5 | 139.5﹣149.5 | 149.5﹣159.5 |
频数 | 2 | 4 | 8 | 7 | 3 | 1 |
根据上面统计信息,解答下列问题: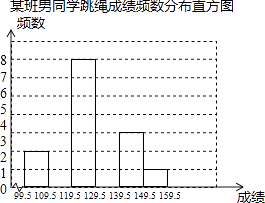
(1)补全频数分布直方图.
(2)班级准备对跳绳成绩优秀的男同学进行奖励,奖励人数占班级男同学的20%,该班张辉同学的成绩为140个,通过计算判断张辉能否获得奖励.
(3)八年级共有200名男同学,若规定男同学的跳绳成绩在120个以上(含120个)为合格,估计该校八年级男同学成绩合格的人数.