题目内容
【题目】给出下列定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形,下列说法:
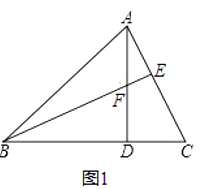
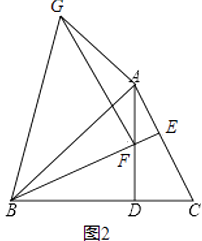
①如图①,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是平行四边形.
②如图②,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH是菱形
③在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,则中点四边形EFGH是正方形
其中,正确的有( )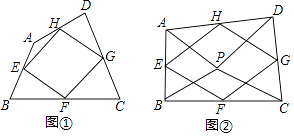
A.0个
B.1个
C.2个
D.3个
【答案】D
【解析】解:如图①,连接AC,BD,
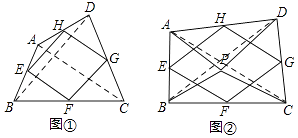
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,
∴EF=HG= ![]() AC,EH=FG=
AC,EH=FG= ![]() BD,
BD,
∴四边形EFGH是平行四边形,故(1)正确;
如图②,连接AC,BD,
∵PA=PB,PC=PD,∠APB=∠CPD,
∴∠BPD=∠APC,
∴△BPD≌△APC,
∴AC=BD,
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,
∴EF=HG= ![]() AC=EH=FG=
AC=EH=FG= ![]() BD,
BD,
∴四边形EFGH是菱形,故(2)正确;
在(2)中增加条件∠APB=∠CPD=90°,其他条件不变,
由△BPD≌△APC,可得∠CAP=∠DBP,
∵△ABP中,∠PAB+∠ABD+∠DBP=90°,
∴∠PAB+∠ABD+∠CAP=90°,
∴AC⊥BD,
由点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,可得EH∥BD,EF∥AC,
∴EH⊥EF,
即∠HEF=90°,
∴菱形EFGH是正方形,故(3)正确,
所以答案是:D.

 名校课堂系列答案
名校课堂系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市![]() 名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
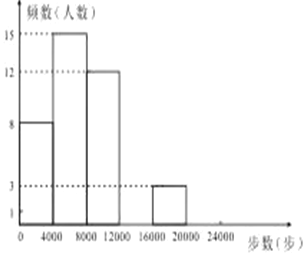
请根据以上信息,解答下列问题:
(1)写出![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(2)本市约有![]() 名教师,用调查的样本数据估计日行走步数超过
名教师,用调查的样本数据估计日行走步数超过![]() 步(包含
步(包含![]() 步)的教师有多少名?
步)的教师有多少名?
(3)若在![]() 名被调查的教师中,选取日行走步数超过
名被调查的教师中,选取日行走步数超过![]() 步(包含
步(包含![]() 步的两名教师与大家分享心得,求被选取的两名教师恰好都在
步的两名教师与大家分享心得,求被选取的两名教师恰好都在![]() 步(包含
步(包含![]() 步)以上的概率.
步)以上的概率.
【题目】在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均数、众数和中位数:
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.