题目内容
【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )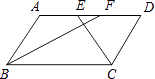
A.8
B.10
C.12
D.14
【答案】B
【解析】解:∵四边形ABCD是平行四边形,
∴AD∥BC,DC=AB=6,AD=BC,
∴∠AFB=∠FBC,
∵BF平分∠ABC,
∴∠ABF=∠FBC,
则∠ABF=∠AFB,
∴AF=AB=6,
同理可证:DE=DC=6,
∵EF=AF+DE﹣AD=2,
即6+6﹣AD=2,
解得:AD=10;
故答案为:B.
根据四边形ABCD是平行四边形,得到AD∥BC,DC=AB=6,AD=BC,∠AFB=∠FBC,又因BF平分∠ABC,得到∠ABF=∠FBC,∠ABF=∠AFB,得到AF=AB=6,同理可证DE=DC=6,因为EF=AF+DE﹣AD=2,即6+6﹣AD=2,得到AD=BC=10.

练习册系列答案
相关题目
【题目】在我市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数,统计数据如下表所示:
册数 | 0 | 1 | 2 | 3 | 4 |
人数 | 3 | 13 | 16 | 17 | 1 |
(1)求这50个样本数据的平均数、众数和中位数:
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
【题目】小亮帮母亲预算家庭4月份电费开支情况,下表是小亮家4月初连续8天每天早上电表显示的读数:
日期/日 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
电表读数/度 | 21 | 24 | 28 | 33 | 39 | 42 | 46 | 49 |
表格中反映的变量是_______,自变量是______,因变量是_______.
