题目内容
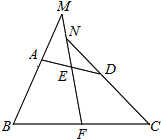
【题目】如图,在四边形ABCD中,E、F分别是AD、BC的中点,连接FE并延长,分别交CD的延长线于点M、N,∠BME=∠CNE,求证:AB=CD.
【答案】证明见解析
【解析】试题分析: 首先连接BD,取BD的中点G,连接EG、FG,证明GE为△ABD的中位线,得到GE=![]() AB;然后同理可证:GF=
AB;然后同理可证:GF=![]() CD,进而得到GE=GF,再结合线段间的等量代换即可解决问题.
CD,进而得到GE=GF,再结合线段间的等量代换即可解决问题.
试题解析:证明:连接BD,取BD的中点G,连接EG、FG.
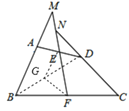
∵点E、G分别为AD、BD的中点,
∴GE为△ABD的中位线,
∴GE=![]() AB.
AB.
同理可证:GF=12CD.
∵GE为△ABD的中位线,
∴GE∥MB,
∴∠GEF=∠BMF.
同理可证:∠GFE=∠CNE.
∵∠BME=∠CNE,
∴∠GEF=∠GFE,
∴GE=GF,
∴AB=CD.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目