题目内容
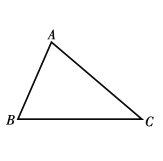
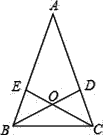
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I, IE⊥B于E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
(AB+BC-AC);④AC=AF+DC.其中正确的结论是_______________ (填序号)
【答案】①②③.
【解析】
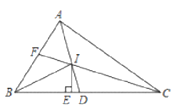
如图,作IM⊥AB于M,IN⊥AC于N.根据角平分线的性质定理以及全等三角形的判定和性质一一判断即可;
如图,作IM⊥AB于M,IN⊥AC于N.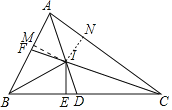
∵AD、CF分别是∠BAC、∠ACB的角平分线,IM⊥AB,IN⊥AC,IE⊥BC,
∴IE=IM=IN,
∴S△ABC=S△ABI+S△ACI+S△BCI=![]() ABIM+
ABIM+![]() ACIN+
ACIN+![]() BCIE=
BCIE=![]() IE(AB+BC+AC),故②正确,
IE(AB+BC+AC),故②正确,
∵∠ABC+∠ACB+∠BAC=180°,∠IBE=![]() ∠ABC,∠IAC=
∠ABC,∠IAC=![]() ∠BAC,∠ICA=
∠BAC,∠ICA=![]() ∠ACB,
∠ACB,
∴∠IBE+∠IAC+∠ICA=90°,
∵∠CID=∠IAC+∠ICA=90°-∠IBE=∠BIE,故①正确,
∵BI=BI,IM=IE,
∴Rt△BIM≌Rt△BIE(HL),
∴BE=BM,同法可证:AM=AN,CN=CE,
∴BE=![]() (AB+BC-AC),故③正确,
(AB+BC-AC),故③正确,
④只有在∠ABC=60°的条件下,AC=AF+DC,故④错误,
故答案为:①②③.

练习册系列答案
相关题目