题目内容
【题目】教材在探索平方差公式时利用了面积法,面积法除了可以帮助我们记忆公式,还可以直观地推导或验证公式,俗称“无字证明”,例如,著名的赵爽弦图(如图①,其中四个直角三角形较大的直角边长都为a,较小的直角边长都为b,斜边长都为c),大正方形的面积可以表示为c2 , 也可以表示为4×![]() ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .
ab+(a-b)2由此推导出重要的勾股定理:如果直角三角形两条直角边长为a,b,斜边长为c,则a2+b2=c2 .

(1)图②为美国第二十任总统伽菲尔德的“总统证法”,请你利用图②推导勾股定理.
(2)如图③,直角△ABC中,∠ACB=90°,AC=3cm,BC=4cm,则斜边AB上的高CD的长为多少?
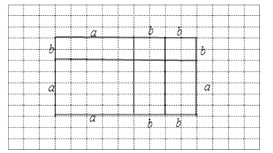
(3)试构造一个图形,使它的面积能够解释(a+b)(a+2b)=a2+3ab+2b2 , 画在如图4的网格中,并标出字母a、b所表示的线段.
【答案】(1)详见解析;(2) ![]() ;(3)详见解析>
;(3)详见解析>
【解析】
(1)梯形的面积可以由梯形的面积公式求出,也利用三个直角三角形面积求出,两次求出的面积相等列出关系式,化简即可得证;
(2)已知两直角边,利用勾股定理求出斜边长,再利用面积法即可求出斜边上的高.
(3)已知图形面积的表达式,即可根据表达式得出图形的边长的表达式,即可画出图形.
解:(1)梯形ABCD的面积为![]() (a+b)(a+b)=
(a+b)(a+b)=![]() a2+ab+
a2+ab+![]() b2 ,
b2 ,
也利用表示为![]() ab+
ab+![]() c2+ab,
c2+ab,
∴![]() a2+ab+
a2+ab+![]() b2=
b2=![]() ab+
ab+![]() c2+
c2+![]() ab,即a2+b2=c2
ab,即a2+b2=c2
(2)∵直角三角形的两直角边分别为3,4,
∴斜边为5,
∵设斜边上的高为h,直角三角形的面积为![]() ×3×4=
×3×4=![]() ×5×h,
×5×h,
∴h=![]() .
.
(3)∵图形面积为:(a+b)(a+2b)=a2+3ab+2b2 ,
∴边长为(a+2b)(a+b),
由此可画出的图形为:

【题目】某校九年级(1)班全体学生初中毕业体育考试的成绩统计如下表:
成绩(分) | 35 | 39 | 42 | 44 | 45 | 48 | 50 |
人数(人) | 2 | 5 | 6 | 6 | 8 | 7 | 6 |
根据上表中的信息判断,下列结论中错误的是( )
A.该班一共有40名同学
B.该班学生这次考试成绩的平均数是45
C.该班学生这次考试成绩的中位数是45
D.该班学生这次考试成绩的众数是45


