题目内容
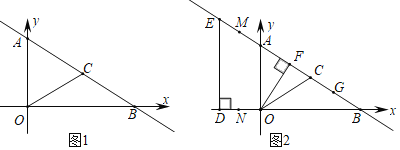
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
x+3分别交y轴,x轴于A、B两点,点C在线段AB上,连接OC,且OC=BC.(1)求线段AC的长度;
(2)如图2,点D的坐标为(﹣![]() ,0),过D作DE⊥BO交直线y=﹣
,0),过D作DE⊥BO交直线y=﹣![]() x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣
x+3于点E.动点N在x轴上从点D向终点O匀速运动,同时动点M在直线=﹣![]() x+3上从某一点向终点G(2
x+3上从某一点向终点G(2![]() ,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
,1)匀速运动,当点N运动到线段DO中点时,点M恰好与点A重合,且它们同时到达终点.
i)当点M在线段EG上时,设EM=s、DN=t,求s与t之间满足的一次函数关系式;
ii)在i)的基础上,连接MN,过点O作OF⊥AB于点F,当MN与△OFC的一边平行时,求所有满足条件的s的值.
【答案】(1)3;(2)i)y=![]() t﹣2;ii)s=
t﹣2;ii)s=![]() 或
或![]() ..
..
【解析】
(1)根据![]() 以及直角三角形斜边中线定理可得点C是AB的中点,即AC=
以及直角三角形斜边中线定理可得点C是AB的中点,即AC=![]() AB,求出点C的坐标和AB的长度,根据AC=
AB,求出点C的坐标和AB的长度,根据AC=![]() AB即可求出线段AC的长度.
AB即可求出线段AC的长度.
(2)i)设s、t的表达式为:①s=kt+b,当t=DN=![]() 时,求出点(
时,求出点(![]() ,2);
,2);
②当t=OD=![]() 时,求出点(
时,求出点(![]() ,6);将点(
,6);将点(![]() ,2)和点(
,2)和点(![]() ,6)代入s=kt+b即可解得函数的表达式.
,6)代入s=kt+b即可解得函数的表达式.
ii)分两种情况进行讨论:①当MN∥OC时,如图1;②当MN∥OF时,如图2,利用特殊三角函数值求解即可.
(1)A、B、C的坐标分别为:(0,3)、(3![]() ,0);
,0);
OC=BC,则点C是AB的中点,则点C的坐标为:(![]() ,
,![]() );
);
故AC=![]() AB=
AB=![]() 6=3;
6=3;
(2)点A、B、C的坐标分别为:(0,3)、(3![]() ,0)、(
,0)、(![]() ,
,![]() );
);
点D、E、G的坐标分别为:(﹣![]() ,0)、(﹣
,0)、(﹣![]() ,4)、(2
,4)、(2![]() ,1);
,1);
i)设s、t的表达式为:s=kt+b,
当t=DN=![]() 时,s=EM=EA=2,即点(
时,s=EM=EA=2,即点(![]() ,2);
,2);
当t=OD=![]() 时,s=EG=6,即点(
时,s=EG=6,即点(![]() ,6);
,6);
将点(![]() ,2)和点(
,2)和点(![]() ,6)代入s=kt+b并解得:
,6)代入s=kt+b并解得:
函数的表达式为:y=![]() t﹣2…①;
t﹣2…①;
ii)直线AB的倾斜角∠ABO=α=30°,EB=8,BD=4![]() ,DE=4,EM=s、DN=t,
,DE=4,EM=s、DN=t,
①当MN∥OC时,如图1,

则∠MNB=∠COB=∠CBO=α=30°,
MN=BM=BE﹣EM=8﹣s,
NH=![]() BN=
BN=![]() (BD﹣DN)=
(BD﹣DN)=![]() (4
(4![]() ﹣t),
﹣t),
cos∠MNH=![]() =
= …②;
…②;
联立①②并解得:s=![]() ;
;
②当MN∥OF时,如图2,
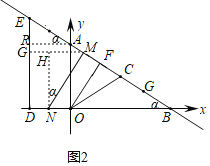
故点M作MG⊥ED角ED于点G,作NH⊥AG于点H,作AR⊥ED于点R,
则∠HNM=∠RAE=∠EBD=α=30°,
HN=GD=ED﹣EG=4﹣EMcos30°=4﹣![]() s,
s,
MH=MG﹣GH=MEcos30°﹣t=![]() s﹣t,
s﹣t,
tanα=![]() =
= …③;
…③;
联立①③并解得:s=![]() ;
;
从图象看MN不可能平行于BC;
综上,s=![]() 或
或![]() .
.