题目内容
)某商场服装部销售一种名牌衬衫,平均每天可售出30件,每件盈利40元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价1元时,平均每天可多卖出2件.
(1)若商场要求该服装部每天盈利1200元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
(1)若商场要求该服装部每天盈利1200元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
(1)设每件应降价x元,由题意可列方程为(40-x)•(30+2x)=1200,
解得x1=0,x2=25,
当x=0时,能卖出30件;
当x=25时,能卖出80件.
根据题意,x=25时能卖出80件,符合题意,不降价也能盈利1200元,符合题意.
因为要减少库存,所以应降价25元.
答:每件衬衫应降价25元;
(2)设商场每天盈利为W元.
W=(40-x)(30+2x)
=-2x2+50x+1200
=-2(x2-25x)+1200
=-2(x-12.5)2+1512.5.
当每件衬衫降价为12或13元时,商场服装部每天盈利最多.
解得x1=0,x2=25,
当x=0时,能卖出30件;
当x=25时,能卖出80件.
根据题意,x=25时能卖出80件,符合题意,不降价也能盈利1200元,符合题意.
因为要减少库存,所以应降价25元.
答:每件衬衫应降价25元;
(2)设商场每天盈利为W元.
W=(40-x)(30+2x)
=-2x2+50x+1200
=-2(x2-25x)+1200
=-2(x-12.5)2+1512.5.
当每件衬衫降价为12或13元时,商场服装部每天盈利最多.
(1)本题的关键语“每件降价1元时,平均每天可多卖出2件”,设每件应降价x元,用x来表示出商场所要求的每件盈利的数额量,然后根据盈利1200元来列出方程;
(2)根据(1)中的方程,然后按一元二次方程的特点,来求出最大值.
(2)根据(1)中的方程,然后按一元二次方程的特点,来求出最大值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
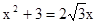 (2)
(2)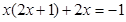

 ,按此计算,一台大型机械设备加工时的实际耗油量为
,按此计算,一台大型机械设备加工时的实际耗油量为 千克。某企业原先一台大型机械设备加工时润滑用油量为90千克,用油的重复利用率为60%。该企业进行了技术革新,发现革新后润滑用油量每减少1千克,用油量的重复利用率将增加2%。这样加工一台大型机械设备的实际耗油量下降到16千克。求:
千克。某企业原先一台大型机械设备加工时润滑用油量为90千克,用油的重复利用率为60%。该企业进行了技术革新,发现革新后润滑用油量每减少1千克,用油量的重复利用率将增加2%。这样加工一台大型机械设备的实际耗油量下降到16千克。求: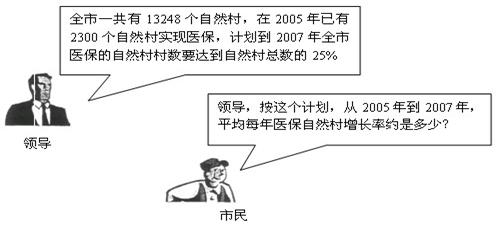
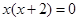 的解是( )
的解是( )

 或
或

 (用配方法);
(用配方法);