题目内容
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

【答案】(1)抛物线解析式为y=﹣x2+4x+5;(2)m的值为7或9;(3)Q点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).
【解析】
试题分析:(1)由A、B的坐标,利用待定系数法可求得抛物线的解析式;
(2)由题意可求得C点坐标,设平移后的点C的对应点为C′,则C′点的纵坐标为8,代入抛物线解析式可求得C′点的坐标,则可求得平移的单位,可求得m的值;
(3)由(2)可求得E点坐标,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,则可证得△PQN≌△EFB,可求得QN,即可求得Q到对称轴的距离,则可求得Q点的横坐标,代入抛物线解析式可求得Q点坐标;当BE为对角线时,由B、E的坐标可求得线段BE的中点坐标,设Q(x,y),由P点的横坐标则可求得Q点的横坐标,代入抛物线解析式可求得Q点的坐标.
试题解析:(1)∵抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点,
∴![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+4x+5;
(2)∵AD=5,且OA=1,
∴OD=6,且CD=8,
∴C(﹣6,8),
设平移后的点C的对应点为C′,则C′点的纵坐标为8,
代入抛物线解析式可得8=﹣x2+4x+5,解得x=1或x=3,
∴C′点的坐标为(1,8)或(3,8),
∵C(﹣6,8),
∴当点C落在抛物线上时,向右平移了7或9个单位,
∴m的值为7或9;
(3)∵y=﹣x2+4x+5=﹣(x﹣2)2+9,
∴抛物线对称轴为x=2,
∴可设P(2,t),
由(2)可知E点坐标为(1,8),
①当BE为平行四边形的边时,连接BE交对称轴于点M,过E作EF⊥x轴于点F,当BE为平行四边形的边时,过Q作对称轴的垂线,垂足为N,如图,
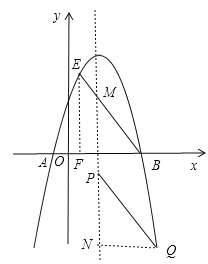
则∠BEF=∠BMP=∠QPN,
在△PQN和△EFB中
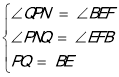
∴△PQN≌△EFB(AAS),
∴NQ=BF=OB﹣OF=5﹣1=4,
设Q(x,y),则QN=|x﹣2|,
∴|x﹣2|=4,解得x=﹣2或x=6,
当x=﹣2或x=6时,代入抛物线解析式可求得y=﹣7,
∴Q点坐标为(﹣2,﹣7)或(6,﹣7);
②当BE为对角线时,
∵B(5,0),E(1,8),
∴线段BE的中点坐标为(3,4),则线段PQ的中点坐标为(3,4),
设Q(x,y),且P(2,t),
∴x+2=3×2,解得x=4,把x=4代入抛物线解析式可求得y=5,
∴Q(4,5);
综上可知Q点的坐标为(﹣2,﹣7)或(6,﹣7)或(4,5).