题目内容
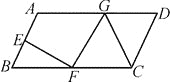
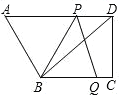
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.
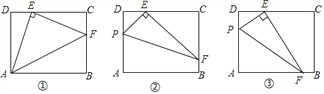
(1)感知:如图①,连接AE,过点E作![]() ,交BC于点F,连接AF,易证:
,交BC于点F,连接AF,易证: ![]() (不需要证明);
(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E ![]() ,交BC于点F,连接PF.求证:
,交BC于点F,连接PF.求证: ![]() 相似;
相似;
(3)应用:如图③,若EF交AB边于点F, ![]() ,其他条件不变,且
,其他条件不变,且![]() 的面积是6,则AP的长为____.
的面积是6,则AP的长为____.
【答案】(1)见解析;(2)证明见解析;(3)![]()
【解析】试题分析:
(1)由已知易证∠AED=∠EFC,∠D=∠C=90°,由AD=3,CD=4结合DE=1可得AD=CE,由此即可证得△AED≌△ECF;
(2)由四边形ABCD是矩形可得∠D=∠C=90°,结合∠PEF=90°可证得∠PED=∠EFC,由此即可证得△PDE∽△ECF;
(3)过点F作FH⊥CD于点H,易得四边形AFHD是矩形,由此可得FH=AD=3,由(2)可得△PDE∽△EHF,由此结合已知条件可证得EF=3PE,结合S△PEF=![]() PE·EF=6,即可解得PE=2,由此在Rt△PDE中解得PD=
PE·EF=6,即可解得PE=2,由此在Rt△PDE中解得PD=![]() ,从而可得AP=AD-PD=
,从而可得AP=AD-PD=![]() .
.
试题解析:
(1)∵四边形ABCD是矩形,EF⊥AE,
∴∠C=∠D=∠AEF=90°,
∴∠DAE+∠AED=90°,∠AED+∠CEF=90°,
∴∠DAE=∠CEF,
∵CD=4,DE=1,AD=3,
∴EC=CD-DE=3=AD,
∴△ADE≌△ECF;
(2)同(1)可得:∠D=∠C,∠DPE=∠CEF,
∴△PDE∽△ECF;
(3)如图3,在矩形ABCD中,过点F作FH⊥CD于点H,
∴∠PHD=∠A=∠D=90°,
∴四边形AFHD是矩形,
∴FH=AD=3,
由(2)可得△PDE∽△EHF,
∴![]() ,
,
∵DE=1,
∴![]() ,即EF=3PE,
,即EF=3PE,
∵S△PEF=![]() PE·EF=6,
PE·EF=6,
∴3PE2=12,解得PE=2,
∴在Rt△PDE中,由勾股定理可得:PD=![]() ,
,
∴AP=AD-PD=![]() .
.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案【题目】某学校2019学年举行席地绘画大赛.共收到绘画作品480件,其中的优秀作品评出了一、二、三等奖.
占获奖总数的几分之几 | 获奖作品的件数 | |
一等奖 |
| b |
二等奖 |
| c |
三等奖 | a | 96 |
(1)则a= ;b= ;c= ;
(2)学校决定为获一等奖同学每人购买一个书包,获得二等奖同学每人购买一个文具盒,获得三等奖同学每人购买一支钢笔,并且每位获奖同学颁发一个证书,已知文具盒单价是书包单价的![]() ,证书的单价是文具盒单价的
,证书的单价是文具盒单价的![]() ,钢笔的单介是文具盒单价的
,钢笔的单介是文具盒单价的![]() ,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
,学校购买书包、文具盒、钢笔共用4000元,那么学校购买证书共用了多少元?
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?