题目内容
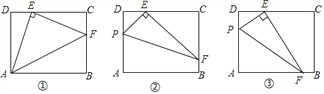
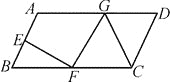
【题目】如图,在平行四边形ABCD中,E,F分别为AB,BC的中点,G是AD 上的任一点.计S1=S△BEF , S2=S△GFC ,S=S□ABCD ,则S=________S2=________S1 .
【答案】4 8
【解析】
设平行四边形BC边上高为h,由中点定义可得BF=CF=![]() BC,BF边上的高为
BC,BF边上的高为![]() h,根据三角形面积公式得S1=S△BEF=
h,根据三角形面积公式得S1=S△BEF=![]() ·BC·h,S2=S△GFC=
·BC·h,S2=S△GFC=![]() ·BC·h,S=S□ABCD=BC·h,从而可得S=4S2=8S1.
·BC·h,S=S□ABCD=BC·h,从而可得S=4S2=8S1.
解:设平行四边形BC边上高为h,
∵ E,F分别为AB,BC的中点,
∴BF=CF=![]() BC,BF边上的高为
BC,BF边上的高为![]() h,
h,
∴S1=S△BEF=![]() ·BF·
·BF·![]() h=
h=![]() ·
·![]() BC·
BC·![]() h=
h=![]() ·BC·h,
·BC·h,
S2=S△GFC=![]() ·CF·h=
·CF·h=![]() ·
·![]() BC·h=
BC·h=![]() ·BC·h,
·BC·h,
S=S□ABCD=BC·h,
∴S=4S2=8S1.
故答案为:4,8.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目