题目内容
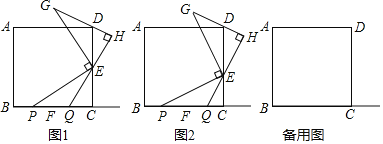
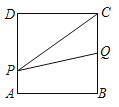
【题目】如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A﹣D﹣C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B﹣C﹣D﹣A的路径向点A运动,当Q到达终点时,P停止移动,设△PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
A.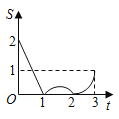 B.
B.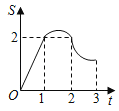
C.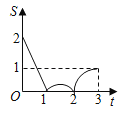 D.
D.
【答案】A
【解析】
分点Q在BC、CD、DA边上,结合图形,分别求出相应的函数解析式,即可进行判断.
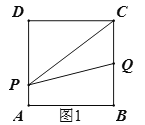
解:当0≤t≤1时,如图1,S=![]() ×2×(2﹣2t)=2﹣2t,∴该段图象是一次函数,且S随t的增大而减小,
×2×(2﹣2t)=2﹣2t,∴该段图象是一次函数,且S随t的增大而减小,
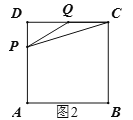
当1<t≤2时,如图2,S=![]() (2﹣t)(2t﹣2)=﹣t2+4t﹣4,∴该段图象是二次函数,且开口向下,
(2﹣t)(2t﹣2)=﹣t2+4t﹣4,∴该段图象是二次函数,且开口向下,
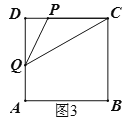
当2<t≤3,如图3,S=![]() (t﹣2)(2t﹣4)=(t﹣2)2,∴该段图象是二次函数,且开口向上.
(t﹣2)(2t﹣4)=(t﹣2)2,∴该段图象是二次函数,且开口向上.
故选:A.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目