Question

【题目】综合与实践

如图，点是正方形的边上一点，点在线段上，将线段绕点顺时针旋转90°得到线段，连接，过点作的垂线，垂足为点，交射线于点．

探究发现

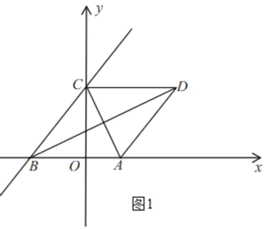
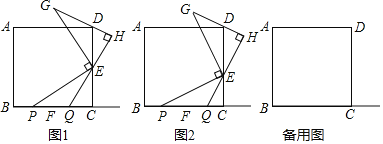
（1）如图1，若点是线段的中点，直接写出线段的数量关系为______；

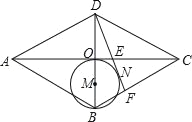
（2）如图2，若点不是线段的中点，线段的数量关系为______，填写出证明过程；

（3）当，时，连接，则________．

Answer 1

【答案】（1）；（2）；过程见解析；（3）9或15．

【解析】

(1)由ASA证明△PEQ≌△EGD，得出PQ=ED，即可得出结论；
(2)由ASA证明△PEQ≌△EGD，得出PQ=ED，即可得出结论；
(3)①当点P在线段BC上时，点Q在线段BC上，由(2)可知：BP=EC-QC，求出DE=2，EC=4，即可得出答案；
②分类讨论，当点Q在线段BC上和点Q在线段BC的延长线上，分别由全等三角形的性质得出BP，即可得出答案．

(1)BP+QC=EC；

理由如下：
∵四边形ABCD是正方形，
∴BC=CD，∠BCD=90°，
由旋转的性质得：∠PEG=90°，EG=EP，
∴∠PEQ+∠GEH=90°，
∵QH⊥GD，
∴∠H=90°，∠G+∠GEH=90°，
∴∠PEQ=∠G，
又∵∠EPQ+∠PEC=90°，∠PEC+∠GED=90°，
∴∠EPQ=∠GED，
在△PEQ和△EGD中，

，
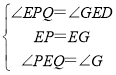∴△PEQ≌△EGD(ASA)，
∴PQ=ED，
∴BP+QC=BC-PQ=CD-ED=EC，
即BP+QC=EC；
故答案为：BP+QC=EC；
(2) BP+QC=EC，

理由如下：
由题意得：∠PEG=90°，EG=EP，
∴∠PEQ+∠GEH=90°，
∵QH⊥GD，
∴∠H=90°，∠G+∠GEH=90°，
∴∠PEQ=∠G，
∵四边形ABCD是正方形，
∴∠DCB=90°，BC=DC，
∴∠EPQ+∠PEC=90°，
∵∠PEC+∠GED=90°，
∴∠GED=∠EPQ，
在△PEQ和△EGD中，

，
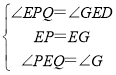∴△PEQ≌△EGD(ASA)，
∴PQ=ED，
∴BP+QC=BC-PQ=CD-ED=EC，
即BP+QC=EC；
(3)分两种情况：
①当点P在线段BC上时，点Q在线段BC上，

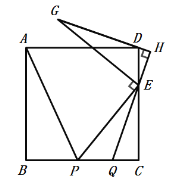
由(2)可知：BP=EC-QC，
∵AB=3DE=6，
∴DE=2，EC=4，
∴BP=4-1=3，

∴；

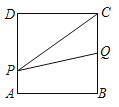
②当点P在线段BC上时，点Q在线段BC的延长线上，如图所示：

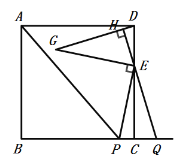
由题意得：∠PEG=90°，EG=EP，
∴∠PEQ+∠GEH=90°，
∵QH⊥GD，
∴∠GHE=90°，∠G+∠GEH=90°，
∴∠PEQ=∠G，
∵四边形ABCD是正方形，
∴∠DCB=90°，BC=DC，
∴∠EPQ+∠PEC=90°，
∵∠PEC+∠GED=90°，
∴∠GED=∠EPQ，
在△PEQ和△EGD中，

，
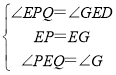∴△PEQ≌△EGD(ASA)，

∴PQ=DE=2，
∵QC=1，
∴PC=PQ-QC=1，
∴BP=BC-PC=6-1=5，

∴；
综上所述，或．