题目内容
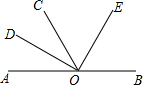
如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.若∠AOC=m°,∠BOC=n°,则∠DOE的度数是______.
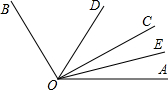

∵OD、OE分别平分∠AOB、∠AOC,∠AOC=m°,∠BOC=n°,
∴∠AOE=∠COE=
∠AOC=
,∠BOC=n°,
又∵∠AOB=m°+n°,
∴∠DOA=
∠AOB=
(m°+n°),
∴∠DOE=
(m°+n°)-
=
.
故答案为:
.
∴∠AOE=∠COE=
| 1 |
| 2 |
| m° |
| 2 |
又∵∠AOB=m°+n°,
∴∠DOA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DOE=
| 1 |
| 2 |
| m° |
| 2 |
| n° |
| 2 |
故答案为:
| n° |
| 2 |

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目