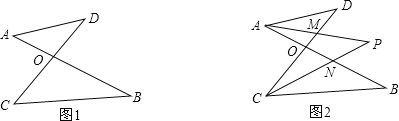题目内容
【题目】如图,直线![]() 与x轴相交于点A,与y轴相交于点B.
与x轴相交于点A,与y轴相交于点B.
(1)求点A,B的坐标;
(2)过点B作直线![]() 与x轴相交于点P,且使
与x轴相交于点P,且使![]() ,求
,求![]() 的面积.
的面积.
(3)如果x轴上有一动点M,要使以A、B、M为顶点的三角形构成为等腰三角形,请探究并求出符合条件的所有M点坐标.

【答案】(1)![]() ;(2)
;(2)![]() 的面积为6或者18;(3)符合条件的所有M点坐标为
的面积为6或者18;(3)符合条件的所有M点坐标为![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
(1)首先令![]() 求出
求出![]() 的值,再令
的值,再令![]() 求出
求出![]() 的值即可得出
的值即可得出![]() 两点的坐标;
两点的坐标;
(2)根据![]() ,要分类讨论点
,要分类讨论点![]() 的方向,点
的方向,点![]() 可以在点
可以在点![]() 的左侧或者右侧两种情况,求出
的左侧或者右侧两种情况,求出![]() 的长,再根据三角形的面积公式求解即可.
的长,再根据三角形的面积公式求解即可.
(3)分三种情况讨论:当A为顶点时、B为顶点时、AB为底边时,求出相应线段,根据点在坐标轴上的位置选择合适的符号,进而写出坐标.
(1)令![]() ,则
,则![]() ,得
,得![]() ,
,
令![]() ,则
,则![]() ,
,
则![]() 两点的坐标为:
两点的坐标为:![]()
(2)分两种情况:①当点P位于y轴左侧时;
![]()
∴![]()
则![]() ;
;
②当点P位于y轴右侧时;
![]()
∴![]()
则![]()
∴![]() 的面积为6或18;
的面积为6或18;
(2)∵![]()
∴![]() ,
,![]() ;∴
;∴![]()
分三种情况:
①当A为顶点时:
![]() 时,则
时,则![]() ,且M在x轴上,
,且M在x轴上,
∴M在A点左侧时,![]() ,∴
,∴![]()
M在A点右侧时,![]() ,∴
,∴![]()
②当B为顶点时:
![]() 时,M位于y轴右侧,∵
时,M位于y轴右侧,∵![]() ,
,
∴![]() ,∴
,∴![]()
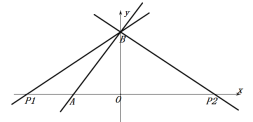
③当AB为底边时:
![]() 时,如图:直线
时,如图:直线![]() 为
为![]() 的垂直平分线,则
的垂直平分线,则![]()
在![]() 中,设
中,设![]()
则![]()
∴由勾股定理得:![]()
∴![]()
解得:![]()
∴![]()
∴![]()
∴符合条件的所有M点坐标为![]() 或
或![]() 或
或![]() 或
或![]()

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目