��Ŀ����
����Ŀ����ͼ1���߶�AB��CD�ཻ�ڵ�O������AD��CB�����ǰ�����ͼ1��ͼ�γ�֮Ϊ��8����������ͼ2����ͼ1�������£���DAB�͡�BCD��ƽ����AP��CP�ཻ�ڵ�P��������CD��AB�ֱ��ཻ��M��N���Խ���������⣺
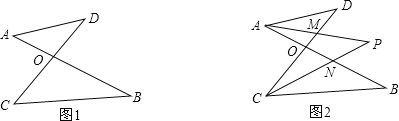
��1����ͼ1�У���ֱ��д����A����B����C����D֮���������ϵ���� ����
��2����ϸ�۲죬��ͼ2����8�������ĸ������� ������
��3��ͼ2�У�����D��40������B��30����ʱ�����P�Ķ�����
���𰸡���1����A+��D����C+��B����2��6����3����P��35��
��������
��1�����������ε��ڽǺͶ�����ʾ����AOD���BOC���ٸ��ݶԶ�����ȿɵá�AOD=��BOC��Ȼ���������ɵý⣻
��2��������8�������Ķ��壬��ϸ�۲�ͼ�μ��ɵó���8����������6����
��3�����ã�1���н��۽�����⼴�ɣ�
�⣺��1���ߡ�A+��D+��AOD����C+��B+��BOC��180������AOD����BOC��
���A+��D����C+��B��
�ʴ�Ϊ��A+��D����C+��B��
��2������8����������6����
�ʴ�Ϊ6��
��3����DAP+��D����P+��DCP���١�PCB+��B����PAB+��P����
�ߡ�DAB����BCD��ƽ����AP��CP�ཻ�ڵ�P��
���DAP����PAB����DCP����PCB��
��+�����DAP+��D+��PCB+��B����P+��DCP+��PAB+��P��
��2��P����D+��B��
���ߡ�D��50�ȣ���B��40�ȣ�
��2��P��40��+30����
���P��35����







