题目内容
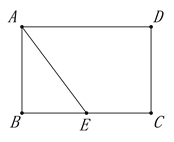
【题目】如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0, ![]() ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
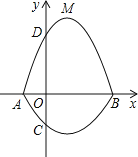
【答案】(1)A(-1,0),B(3,0);(2)![]() ;(3)当P点坐标为(
;(3)当P点坐标为(![]() ,
, ![]() )时,
)时, ![]() 有最大值,
有最大值, ![]() .
.
【解析】试题分析:(1)把抛物线解析整理,令y=0可求得x的值,则可求得A、B的坐标;
(2)由A、B、C的坐标,利用待定系数法可求得经过点A、B、C的抛物线解析式;
(3)连接BC、过点P作PQ∥y轴,交BC于点Q,由B、C的坐标可求得直线BC的解析式,则可设出P点坐标,从而表示出Q点坐标,则可求得PQ的长,从而用P点坐标表示出△PBC的面积,利用二次函数的性质可求得P点坐标和△PBC面积的最大值.
试题解析:解:(1)∵y=mx2-2mx-3m=m(x-3)(x+1),且m≠0,
∴当y=0时,可得m(x-3)(x+1)=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)设过A、B、C三点的抛物线解析式为y=ax2+bx+c,
则有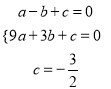 ,解得
,解得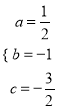 ,
,
∴抛物线C1解析式为![]() ;
;
(3)如图,过点P作PQ∥y轴,交BC于Q,
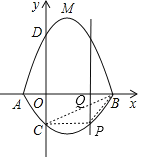
设直线BC解析式为y=kx+s,则有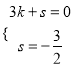 ,解得
,解得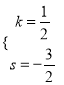 ,
,
∴ 直线BC的解析式为![]() ,
,
设P(x, ![]() ),则Q(x,
),则Q(x, ![]() ),
),
∴ PQ= ![]() ,
,
∴ S△PBC=![]() PQOB=
PQOB=![]() ×(
×(![]() x2+
x2+![]() x)×3=
x)×3=![]() (x
(x![]() )2+
)2+![]() ,
,
∵![]() <0,
<0,
∴ 当x=![]() 时,S△PBC有最大值,S最大=
时,S△PBC有最大值,S最大=![]() ,此时P点纵坐标为
,此时P点纵坐标为![]() ,
,
∴ 此时P点坐标为(![]() ,
, ![]() ).
).

【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由