题目内容
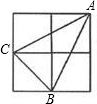 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:以AC、AB、BC为斜边的三个直角三角形的面积分别为1、1、
,因此△ABC的面积为
;用勾股定理计算AC的长为
,因此AC边上的高为
.
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 3 |
| 5 |
| 5 |
解答:解:∵三角形的面积等于小正方形的面积减去三个直角三角形的面积,即S△ABC=4-
×1×2-
×1×1-
×1×2=
∵AC=
=
,
∴AC边上的高=
=
,
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵AC=
| 12+22 |
| 5 |
∴AC边上的高=
| 3 | ||
|
| 3 |
| 5 |
| 5 |
故选C.
点评:此题首先根据大正方形的面积减去三个直角三角形的面积计算,再根据勾股定理求得AC的长,最后根据三角形的面积公式计算.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.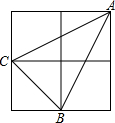 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
 如图,小正方形边长为1,则△ABC中AC边上的高等于
如图,小正方形边长为1,则△ABC中AC边上的高等于