题目内容
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.(1)求△ABC的面积;
(2)求AC边上的高.
分析:(1)三角形的面积等于四个小正方形的面积减去△ABC之外的三个三角形的面积;
(2)先求出BC边的长,再利用面积就可求出AC边上的高.
(2)先求出BC边的长,再利用面积就可求出AC边上的高.
解答:解:(1)S△ABC=1×4-
×1×2-
×1×1-
×1×2=
;
(2)AC=
=
,
设高为h,
则
AC•h=
,
解得h=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
(2)AC=
| 12+22 |
| 5 |
设高为h,
则
| 1 |
| 2 |
| 3 |
| 2 |
解得h=
| 3 |
| 5 |
| 5 |
点评:本题主要考查图象识别,从图象中分析出面积的计算,题目得以解决;另外,勾股定理也是考查点之一.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
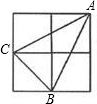 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
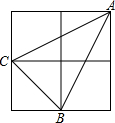 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
 如图,小正方形边长为1,则△ABC中AC边上的高等于
如图,小正方形边长为1,则△ABC中AC边上的高等于