题目内容
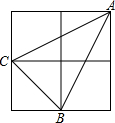 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高长度为分析:求出三角形ABC的面积,再根据三角形的面积公式即可求得AC边上的高.
解答: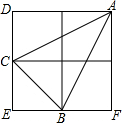 解:四边形DEFA是正方形,面积是4;
解:四边形DEFA是正方形,面积是4;
△ABF,△ACD的面积相等,且都是
×1×2=1.
△BCE的面积是:
×1×1=
.
则△ABC的面积是:4-1-1-
=
.
在直角△ADC中根据勾股定理得到:AC=
=
.
设AC边上的高线长是x.则
AC•x=
x=
,
解得:x=
.
 解:四边形DEFA是正方形,面积是4;
解:四边形DEFA是正方形,面积是4;△ABF,△ACD的面积相等,且都是
| 1 |
| 2 |
△BCE的面积是:
| 1 |
| 2 |
| 1 |
| 2 |
则△ABC的面积是:4-1-1-
| 1 |
| 2 |
| 3 |
| 2 |
在直角△ADC中根据勾股定理得到:AC=
| 22+12 |
| 5 |
设AC边上的高线长是x.则
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
解得:x=
| 3 |
| 5 |
| 5 |
点评:求△ABC的面积要用正方形的面积减去三个直角三角形的面积是解决本题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
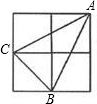 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC.
 如图,小正方形边长为1,则△ABC中AC边上的高等于
如图,小正方形边长为1,则△ABC中AC边上的高等于