题目内容
【题目】若数a使关于x的分式方程 
+ 
=4的解为正数，且使关于y的不等式组 
的解集为y＜﹣2，则符合条件的所有整数a的和为（ ）
A.10
B.12
C.14
D.16
【答案】B
【解析】解：分式方程 
+ 
=4的解为x= 
且x≠1， ∵关于x的分式方程 + =4的解为正数，
∴ ＞0且 ≠1，
∴a＜6且a≠2．
，
解不等式①得：y＜﹣2；
解不等式②得：y≤a．
∵关于y的不等式组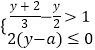 
的解集为y＜﹣2，
∴a≥﹣2．
∴﹣2≤a＜6且a≠2．
∵a为整数，
∴a=﹣2、﹣1、0、1、3、4、5，
（﹣2）+（﹣1）+0+1+3+4+5=10．
故选B．
【考点精析】根据题目的已知条件，利用分式方程的解和一元一次不等式组的解法的相关知识可以得到问题的答案，需要掌握分式方程无解（转化成整式方程来解,产生了增根;转化的整式方程无解）；解的正负情况:先化为整式方程,求整式方程的解；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．
【题目】某公司生产的某种产品每件成本为40元，经市场调查整理出如下信息：
①该产品90天内日销售量（m件）与时间（第x天）满足一次函数关系，部分数据如下表：
时间（第x天） | 1 | 3 | 6 | 10 | … |
日销售量（m件） | 198 | 194 | 188 | 180 | … |
②该产品90天内每天的销售价格与时间（第x天）的关系如下表：
时间（第x天） | 1≤x＜50 | 50≤x≤90 |
销售价格（元/件） | x+60 | 100 |
（1）求m关于x的一次函数表达式；
（2）设销售该产品每天利润为y元，请写出y关于x的函数表达式，并求出在90天内该产品哪天的销售利润最大？最大利润是多少？【提示：每天销售利润=日销售量×（每件销售价格﹣每件成本）】
（3）在该产品销售的过程中，共有多少天销售利润不低于5400元，请直接写出结果．
