题目内容
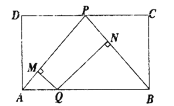
【题目】如图,正方形![]() 的边长为 1 ,
的边长为 1 , ![]() 是对角线 . 将
是对角线 . 将![]() 绕着点 D 顺时针旋转
绕着点 D 顺时针旋转![]() 得到
得到![]() 交
交![]() 于点 E ,连接
于点 E ,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() . 下列结论: ①
. 下列结论: ①![]() ;②
;②![]() ; ③
; ③![]() ; ④
; ④![]() . 其中结论正确的个数是( )
. 其中结论正确的个数是( )
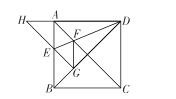
A.1 个B.2 个C.3 个D.4 个
【答案】C
【解析】
由旋转可以得到△DCB≌△DGH,故有DB=DH=![]() ,且∠H =45°,推出△AHE为等腰直角三角形,由∠EBG=45°,推出△EGB也为等腰直角三角形,且HE=BE,推出△AEH≌△GEB;由△AFD∽△HED,求出AF=
,且∠H =45°,推出△AHE为等腰直角三角形,由∠EBG=45°,推出△EGB也为等腰直角三角形,且HE=BE,推出△AEH≌△GEB;由△AFD∽△HED,求出AF=![]() =EG,推出四边形AFGE是平行四边形,由AE=EG,推出四边形AFGE是菱形,由此可以求出∠AFG=∠AEG=135°,由此可以求出AB+AF=
=EG,推出四边形AFGE是平行四边形,由AE=EG,推出四边形AFGE是菱形,由此可以求出∠AFG=∠AEG=135°,由此可以求出AB+AF=![]() .
.
解:∵△DCB绕点D旋转45°得到△DGH,∴△DCB≌△DGH,
∴ DB=DH=![]() ,且∠H=∠DBC=45°,
,且∠H=∠DBC=45°,
∴△AHE为等腰直角三角形,∴ AE=AH=DH-AD=![]() ,
,
BE=AB-AE=![]() ,
,
∵∠AEH=∠BEG=45°,∠EBG=45°,
∴△EGB也为等腰直角三角形,EG=![]() ,∴EG=AE,
,∴EG=AE,
∴ △AEH≌△GEB,∴AE=EG,故②正确
设AC与BD相交于O点,又∠DGB=90°=∠AOB=90°,
∴EG∥AO,故△AFD∽△HED,∴![]() ,
,![]()
∴AF=![]() =EG,∴四边形AFGE为平行四边形,且AE=EG
=EG,∴四边形AFGE为平行四边形,且AE=EG
∴四边形AFGE为菱形,故有FG=EG,故①正确;
∵四边形AFGE为菱形,
∴∠AFG=∠AEG=180°-∠BEG=180°-45°=135°,故③正确;
AB+AF=![]() ,故④错误.
,故④错误.
故答案选:C.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
【题目】某水果店经销进价分别为![]() 元/千克、
元/千克、![]() 元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
元/千克的甲、乙两种水果,下表是近两天的销售情况:(进价、售价均保持不变,利润=售价-进价)
时间 | 甲水果销量 | 乙水果销量 | 销售收入 |
周五 |
|
|
|
周六 |
|
|
|
(1)求甲、乙两种水果的销售单价;
(2)若水果店准备用不多于![]() 元的资金再购进两种水果共
元的资金再购进两种水果共![]() 千克,求最多能够进甲水果多少千克?
千克,求最多能够进甲水果多少千克?
(3)在(2)的条件下,水果店销售完这![]() 千克水果能否实现利润为
千克水果能否实现利润为![]() 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
元的目标?若能,请给出相应的采购方案;若不能,请说明理由.