题目内容
【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,求F、C两点的距离
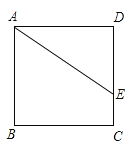
【答案】1或5.
【解析】试题分析:根据正方形的性质可得AB=AD,∠ABC=∠D=90°,再根据旋转的性质可得AF=AE,然后利用“HL”证明Rt△ABF和Rt△ADE全等,根据全等三角形对应边相等可得BF=DE,再求出正方形的边长为3,然后分点F在线段BC上和CB的延长线上两种情况讨论求解.
试题解析:
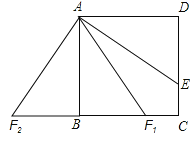
解:顺时针旋转得到F1点,
∵AE=AF1,AD=AB,∠D=∠ABC=90°,
∴△ADE≌△ABF1,
∴F1C=1;
逆时针旋转得到F2点,同理可得△ABF2≌△ADE,
∴F2B=DE=2,
F2C=F2B+BC=5.
综上所述,F、C两点间的距离为1或5.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
【题目】某学习小组在研究函数y=![]() x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x3﹣2x的图象与性质时,已列表、描点并画出了图象的一部分.
x | … | ﹣4 | ﹣3.5 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
y | … | ﹣ | ﹣ |
|
|
| 0 | ﹣ | ﹣ | ﹣ |
|
| … |
(1)请补全函数图象;
(2)方程![]() x3﹣2x=﹣2实数根的个数为 ;
x3﹣2x=﹣2实数根的个数为 ;
(3)观察图象,写出该函数的两条性质.