Question

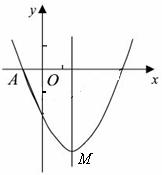
如图，点A(－1，0)为二次函数y＝x²＋bx－2的图象与x轴的一个交点．

(1)求该二次函数的表达式，并说明当x＞0时，y值随x值变化而变化的情况；

(2)将该二次函数图象沿x轴向右平移1个单位，请直接写出平移后的图象与x轴的交点坐标．

Answer 1

 (1)∵点A(－1，0)在抛物线y＝x² ＋ bx－2上，

∴× (－1 )² ＋ b× (－1) –2 ＝ 0，解得b ＝－．……1分

∴抛物线的解析式为y＝x²－x－2．……2分

∴抛物线的对称轴为过点(，0)与y轴平行的直线，

∴当0＜x≤时，y值随x值增大而减小；当x＞时，y值随x值增大而增大．……4分

(2) ∵原抛物线与x轴的交点坐标分别为(－1，0 )，(4，0 )，

∴平移后的图象与x轴的交点坐标分别为(0，0 )，(5，0 )．……6分(不写理由不扣分)