��Ŀ����
����Ŀ����ͼ��ֱ��y=![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+![]() x+c����B��C���㣮
x+c����B��C���㣮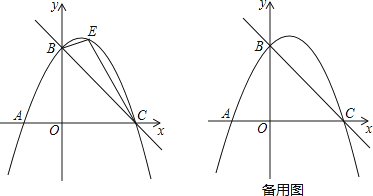
��1���������ߵĽ���ʽ��
��2����ͼ����E��ֱ��BC�Ϸ��������ϵ�һ���㣬����BEC������ʱ���������E������͡�BEC��������ֵ��
��3���ڣ�2���Ľ����£�����E��y���ƽ���߽�ֱ��BC�ڵ�M������AM����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��ֱ��y=![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��
���B�������ǣ�0��3������C�������ǣ�4��0����
��������y=ax2+![]() x+c����B��C���㣬
x+c����B��C���㣬
��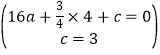
���
��y=![]() .
.
��2��
�⣺��ͼ1������E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F��
 ��
��
�ߵ�E��ֱ��BC�Ϸ��������ϵ�һ���㣬
�����E�������ǣ�x��![]() ����
����
���M�������ǣ�x��![]() x+3����
x+3����
��EM=![]() ����
����![]() +3��=
+3��=![]() x2+
x2+![]() x��
x��
��S��BEC=S��BEM+S��MEC
=![]()
=![]() ����
����![]() ����4
����4
=![]() x2+3x
x2+3x
=![]() ��x��2��2+3��
��x��2��2+3��
�൱x=2ʱ������E�������ǣ�2��3��ʱ����BEC����������������3��
��3��
�⣺���������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�
����ͼ2��
 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2��![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ�![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:

��� ��
��
��x��0��
���P�������ǣ���3��![]() ����
����
����ͼ3��
 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2�� ![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ� ![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:
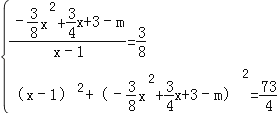
��� ��
��
��x��0��
���P�������ǣ�5��![]() ����
����
����ͼ4��
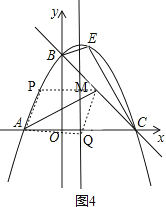 ��
��
�ɣ�2�����ɵõ�M�ĺ�������2��
�ߵ�M��ֱ��y=![]() x+3�ϣ�
x+3�ϣ�
���M�������ǣ�2�� ![]() ����
����
�֡ߵ�A�������ǣ���2��0����
��AM=![]() =
= ![]() ��
��
��AM���ڵ�ֱ�ߵ�б���ǣ� ![]() =
=![]() ��
��
��y=![]() x2+
x2+ ![]() x+3�ĶԳ�����x=1��
x+3�ĶԳ�����x=1��
�����Q�������ǣ�1��m������P�������ǣ�x��![]() x2+
x2+ ![]() x+3������:
x+3������:

���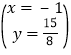
���P�������ǣ���1�� ![]() ����
����
���ϣ��ɵ�
���������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�
��P�������ǣ���3��![]() ������5��
������5��![]() ��������1��
��������1�� ![]() ����
����
����������1�����ȸ���ֱ��y=��![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B�������B�������ǣ�0��3������C�������ǣ�4��0����Ȼ�����������y=ax2+
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B�������B�������ǣ�0��3������C�������ǣ�4��0����Ȼ�����������y=ax2+![]() x+c����B��C���㣬���a\c��ֵ�Ƕ��٣�������������ߵĽ���ʽ��
x+c����B��C���㣬���a\c��ֵ�Ƕ��٣�������������ߵĽ���ʽ��
��2�����ȹ���E��y���ƽ����EF��ֱ��BC�ڵ�M��EF��x���ڵ�F��Ȼ�����E�������ǣ�x����![]() x2+
x2+![]() x+3�������M�������ǣ�x����
x+3�������M�������ǣ�x����![]() x+3�������EM��ֵ�Ƕ��٣������������ε�����������S��ABC �� �����жϳ�����BEC������ʱ����E������͡�BEC��������ֵ���Ƕ��ټ��ɣ�
x+3�������EM��ֵ�Ƕ��٣������������ε�����������S��ABC �� �����жϳ�����BEC������ʱ����E������͡�BEC��������ֵ���Ƕ��ټ��ɣ�
��3�����������ϴ��ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�Ȼ�������������ۣ�����ƽ���ı��ε����������ʹ����P��Q��A��MΪ������ı�����ƽ���ı��εĵ�P�������Ƕ��ټ��ɣ�
�����㾫�������ö��κ�������ֵ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪����Ա�����ȡֵ��Χ��ȫ��ʵ������ô�����ڶ��㴦ȡ�����ֵ������Сֵ��������x=-b/2aʱ��y��ֵ=(4ac-b2)/4a��







