Question

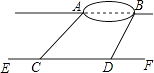
【题目】如图，已知等边△ABC，D是边BC的中点，过D作DE∥AB于E，连接BE交AD于D1；过D1作D1E1∥AB于E1 ， 连接BE1交AD于D2；过D2作D2E2∥AB于E2 ， …，如此继续，若记S△BDE为S1 ， 记 为S2 ， 记 为S3…，若S△ABC面积为Scm，则Sn=cm（用含n与S的代数式表示）

Answer 1

【答案】
【解析】解：∵D是边BC的中点，过D作DE∥AB，
∴E为AC的中点，BE⊥AC，
设△ABC的高是h，

过E作EM⊥BC于M，
∵BD=DC，DE∥AB，
∴AE=EC，
∵AD⊥BC，EM⊥BC，
∴AD∥EM，
∴DM=MC，
∴EM= AD= h，∴s1= BC AD= s= ，
∵DE∥AB，D1E1∥AB，
∴ = =2= ，∴s2= AEh﹣ AE h= s= ，同理s3= ，s= ，
…
sn= ，所以答案是： ．
【考点精析】掌握三角形的面积和等边三角形的性质是解答本题的根本，需要知道三角形的面积=1/2×底×高；等边三角形的三个角都相等并且每个角都是60°．