题目内容
证明题:如图以△ABC边AB为直径作⊙O交BC于D,已知BD=DC,

⑴求证:△ABC是等腰三角形
⑵若:∠A=36°,求弧AD的度数

⑴求证:△ABC是等腰三角形
⑵若:∠A=36°,求弧AD的度数
(1)证明过程如下;(2)144°.
试题分析:(1)连接AD,由AB是⊙O的直径,得到∠ADB=90°,而BD=CD,得到△ABD是等腰三角形;
(2)由∠A=36°,△ABD是等腰三角形,可得∠B,由此得到AD弧的度数.
试题解析:(1)证明:如图,连接AD,

∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
又∵BD=CD,
∴△ABC是等腰三角形;
(2)解:∵∠A=36°,
∴∠B=∠C=
 (180°-∠A)=72°
(180°-∠A)=72°所以弧AD的度数等于72°×2=144°.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目

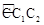 的长是 (保留π).
的长是 (保留π).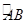 上一点(不与A、B重合),则
上一点(不与A、B重合),则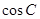 的值为 .
的值为 .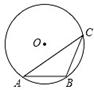
 ,母线长为4
,母线长为4 是劣弧
是劣弧 的2倍;⑤AE=BC.其中正确结论的序号是 .
的2倍;⑤AE=BC.其中正确结论的序号是 .