��Ŀ����
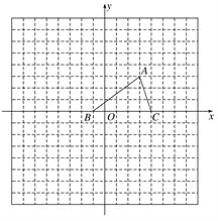
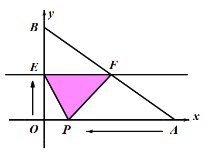
����Ŀ����ͼ����֪A��B���������ֱ�Ϊ(40��0)��(0��30)������P�ӵ�A��ʼ���߶�AO����ÿ��2����λ���ȵ��ٶ���ԭ��O�˶���ͬʱֱ��EF��x��Ϊ��ʼλ����ÿ��1����λ���ȵ��ٶ�����ƽ���ƶ�(��EF��x��)�����ҷֱ���y�ᡢ�߶�AB���ڵ�E��F������EP��FP���趯��P��ֱ��EFͬʱ�������˶�ʱ��Ϊt����
��1����t=15��ʱ����EF�ij�����
��2��ֱ��EF����P���˶����������Ƿ����������t��ʹ����PEF���������160(ƽ����λ)?���������������ʱ��ֵ��������������˵��������
���𰸡���1��EF=20����2��������ʹ��![]() ���������
���������![]() ��ƽ����λ����
��ƽ����λ����![]() ֵ.
ֵ.
��������
��1����t=15ʱ��OE=15����֤��BEF�ס�BOA����![]() ���Ӷ����EF�ij�����
���Ӷ����EF�ij�����
��2���������������t��ʹ�á�PEF���������160������������ʽ�г��������ɸ����б�ʽ�����ж����ó�������
��1����EF��OA�����BEF=��BOA��
�֡ߡ�B=��B�����BEF�ס�BOA����![]() ����t=15ʱ��OE=BE=15��OA=40��OB=30����
����t=15ʱ��OE=BE=15��OA=40��OB=30����![]() ��
��
��2���ߡ�BEF�ס�BOA����![]() ����
����![]() ����������t2��30t+240=0��
����������t2��30t+240=0��
�ߡ�=302��4��1��240=��60��0�����û��ʵ�����������ʹ�á�PEF���������160��ƽ����λ����tֵ��

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�