题目内容
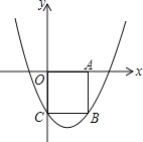
【题目】如图,在平面直角坐标系xOy中,边长为2的正方形OABC的顶点A、C分别在x轴正半轴、y轴的负半轴上,二次函数y=![]() (xh)2+k的图象经过B、C两点.
(xh)2+k的图象经过B、C两点.
(1)求该二次函数的顶点坐标;
(2)结合函数的图象探索:当y>0时x的取值范围;
(3)设m<![]() ,且A(m,y1),B(m+1,y2)两点都在该函数图象上,试比较y1、y2的大小,并简要说明理由.
,且A(m,y1),B(m+1,y2)两点都在该函数图象上,试比较y1、y2的大小,并简要说明理由.
【答案】(1)二次函数的顶点坐标为(1,-![]() );(2)x<-1或x>3;(3)y1>y2.
);(2)x<-1或x>3;(3)y1>y2.
【解析】
(1)根据正方形的性质得出点B、C的坐标,根据二次函数的对称性得出h的数值,再进一步代入一点求出k的数值,即可求出顶点坐标;
(2)由(1)函数解析式求出与x轴交点的坐标解决问题;
(3)根据二次函数的对称性与点A(m,y1)对称的点为(2-m,y1),根据图形,比较得出结论.
解:(1)∵正方形OABC的边长为2,
∴点B、C的坐标分别为(2,-2),(0,-2),对称轴x=h=![]() =1,
=1,
把C(0,-2)代入二次函数y=![]() +k,解得k= -
+k,解得k= -![]() ;
;
∴二次函数的顶点坐标为(1,-![]() );
);
(2)当y=0时,![]() =0,解得
=0,解得![]() =-1,
=-1,![]() =3,
=3,
∴当y>0时,x<-1或x>3;
(3)点A(m,y1)关于x=1对称点为(2-m,y1),
∵m<![]() ,
,
∴m+1<2-m,
∴y1>y2.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案【题目】某商贸公司购进某种水果的成本为20元/千克,经过市场调研发现,这种水果在未来48天的售价p(元/千克)与时间t(天)之间的函数表达式为
p=
且其日销售量y(kg)与时间t(天)的关系如下表:
时间t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日销售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y与t之间的变化规律符合一次函数关系,试求第30天的日销售量是多少?
(2)问:哪一天的销售利润最大?最大日销售利润为多少?
(3)在实际销售的前24天中,公司决定每销售1 kg水果就捐赠n元利润(n<9)给“精准扶贫”对象.现发现:在前24天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求n的取值范围.
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.