题目内容
如图,已知二次函数图象的顶点为原点,直线y=| 1 | 2 |
(1)求B点的坐标与这个二次函数的解析式;
(2)P为线段AB上的一个动点(点P与A、B不重合),过P点作x轴的垂线与这个二次函数的图象交于D点,与x轴交于点E.设该线段PD的长为h,点P的横坐标为t,求h与t之间的函数解析式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段AB上是否存在点P,使得以点P、D、B为顶点的三角形与△B
 OC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
OC相似?若存在,请求出P点的坐标;若不存在,请说明理由.
分析:(1)根据二次函数的顶点为原点,得出二次函数的一般解析式y=ax2,将(8,8)代入即可;
(2)直接表示出PE与DE的长度从而得出PD的长,即可得出解析式;
(3)分别为当∠PDB=∠BOC=90°时与当∠PDB=∠BOC=90°时,利用相似三角形的判定与性质求出即可.
(2)直接表示出PE与DE的长度从而得出PD的长,即可得出解析式;
(3)分别为当∠PDB=∠BOC=90°时与当∠PDB=∠BOC=90°时,利用相似三角形的判定与性质求出即可.
解答:解:(1)令x=0,代入y=
x+4,
∴y=4,
∴B(0,4).
设y=ax2,把(8,8)代入得:82•a=8,
∴a=
,
∴y=
x2,
(2)∵点P的横坐标为t,
∴PE=
t+4;DE=
t2.
∴PD=PE-DE=
t+4-
t2,
∴h=-
t2+
t+4(0<t<8);
(3)存在,
①当∠PDB=∠BOC=90°时,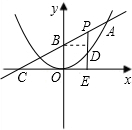
∴BD∥CE,
∴∠PBD=∠BCO.
∴△PDB∽△BOC,
∴
=
.
令y=
x=4=0,得x=-8,
∴C(-8,0),
∴CO=8.
∴
=
.
化简得:t2=32.
解得:t1=4
;t2=-4
<0(不合题意,舍去).
把t1=4
代入y=
x+4,
得y=2
+4.
∴点P的坐标为(4
,2
+4).
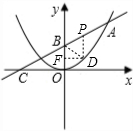
②当∠PBD=∠BOC=90°时,
∵PD∥BO,∴∠DPB=∠CBO.
∴△PBD∽△BOC.
过点D作DF⊥OB,
∵∠DPB+∠PDB=90°,∠BDF+∠PDB=90°,
∴∠BDF=∠DPB=∠CBO.
∵∠BFD=∠COB,
△DFB∽△BOC,
∵BF=BO-OF=4-
t2,
∴
=
,
∴
=
.
化简得:t2+16t-32=0.
解得:t1=-8+4
;t2=-8-4
<0(不合题意,舍去)
把t1=-8+4
代入y=
x+4,
得:y=2
,
∴P点的坐标为(-8+4
,2
),
∴当P点的坐标为(-8+4
,2
)或(4
,2
+4)时
以点P.D.B为顶点的三角形与△BOC相似.
| 1 |
| 2 |
∴y=4,
∴B(0,4).
设y=ax2,把(8,8)代入得:82•a=8,
∴a=
| 1 |
| 8 |
∴y=
| 1 |
| 8 |
(2)∵点P的横坐标为t,
∴PE=
| 1 |
| 2 |
| 1 |
| 8 |
∴PD=PE-DE=
| 1 |
| 2 |
| 1 |
| 8 |
∴h=-
| 1 |
| 8 |
| 1 |
| 2 |
(3)存在,
①当∠PDB=∠BOC=90°时,

∴BD∥CE,
∴∠PBD=∠BCO.
∴△PDB∽△BOC,
∴
| PD |
| BO |
| BD |
| CO |
令y=
| 1 |
| 2 |
∴C(-8,0),
∴CO=8.
∴
-
| ||||
| 4 |
| t |
| 8 |
化简得:t2=32.
解得:t1=4
| 2 |
| 2 |
把t1=4
| 2 |
| 1 |
| 2 |
得y=2
| 2 |
∴点P的坐标为(4
| 2 |
| 2 |
②当∠PBD=∠BOC=90°时,
∵PD∥BO,∴∠DPB=∠CBO.
∴△PBD∽△BOC.
过点D作DF⊥OB,
∵∠DPB+∠PDB=90°,∠BDF+∠PDB=90°,
∴∠BDF=∠DPB=∠CBO.
∵∠BFD=∠COB,
△DFB∽△BOC,
∵BF=BO-OF=4-
| 1 |
| 8 |
∴
| DF |
| BO |
| BF |
| CO |

∴
| t |
| 4 |
4-
| ||
| 8 |
化简得:t2+16t-32=0.
解得:t1=-8+4
| 6 |
| 6 |
把t1=-8+4
| 6 |
| 1 |
| 2 |
得:y=2
| 6 |
∴P点的坐标为(-8+4
| 6 |
| 6 |
∴当P点的坐标为(-8+4
| 6 |
| 6 |
| 2 |
| 2 |
以点P.D.B为顶点的三角形与△BOC相似.
点评:此题主要考查了二次函数的综合应用以及相似三角形的判定等知识,熟练应用相似三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
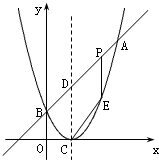 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+m与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在轴y上.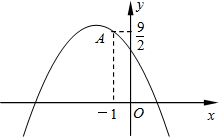 (2012•高淳县一模)如图,已知二次函数y=-
(2012•高淳县一模)如图,已知二次函数y=-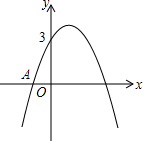 (2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
(2013•江宁区二模)如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
 如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.
如图,已知二次函数y=(x-1)2的图象的顶点为C点,图象与直线y=x+m的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上.