题目内容
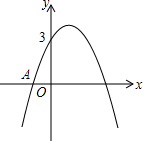（2013•江宁区二模）如图，已知二次函数y=ax2+bx+3的图象过点A（-1，0），对称轴为过点（1，0）且与y轴平行的直线．（1）求该二次函数的关系式；
（2）结合图象，解答下列问题：
①当x取什么值时，该函数的图象在x轴上方？
②当-1＜x＜2时，求函数y的取值范围．
分析：（1）将A坐标代入二次函数解析式中，利用对称轴公式列出关系式，联立求出a与b的值，即可确定出二次函数解析式；
（2）①由二次函数图象与x轴的交点及对称轴求出另一个交点坐标，利用图象即可得出，该函数的图象在x轴上方时x的范围；
②根据二次函数的性质求出y的最大值，根据x的范围即可确定出y的范围．
（2）①由二次函数图象与x轴的交点及对称轴求出另一个交点坐标，利用图象即可得出，该函数的图象在x轴上方时x的范围；
②根据二次函数的性质求出y的最大值，根据x的范围即可确定出y的范围．
解答：解：（1）根据题意可得：
，
解得：
，
则二次函数解析式为y=-x2+2x+3=-（x-1）2+4；
（2）∵函数图象与x轴的一个交点坐标为A（-1，0），且对称轴为直线x=1，
∴函数图象与x轴的另一个交点为（3，0），
∴当-1＜x＜3 时，该函数的图象在x轴上方；
（3）∵函数的顶点坐标为（1，4），
∴当x=1时，y的最大值为4，
∴当-1＜x＜2时，函数y的取值范围为0＜y≤4．
|
解得：
|
则二次函数解析式为y=-x2+2x+3=-（x-1）2+4；
（2）∵函数图象与x轴的一个交点坐标为A（-1，0），且对称轴为直线x=1，
∴函数图象与x轴的另一个交点为（3，0），
∴当-1＜x＜3 时，该函数的图象在x轴上方；
（3）∵函数的顶点坐标为（1，4），
∴当x=1时，y的最大值为4，
∴当-1＜x＜2时，函数y的取值范围为0＜y≤4．
点评：此题考查了待定系数法求二次函数解析式，以及二次函数的性质，熟练掌握待定系数法是解本题的关键．
练习册系列答案
相关题目
（2013•江宁区二模）甲、乙两名同学在一次用频率去估计概率的实验中，统计了某一结果出现的频率绘出的统计图如图所示，则符合这一结果的实验可能是（ ）
（2013•江宁区二模）如图，若将木条a绕点O旋转后与木条b平行，则旋转角的最小值为
（2013•江宁区二模）在如图所示的5×5方格中，每个小方格都是边长为1的正方形，△ABC是格点三角形（即顶点恰好是正方形的顶点），将△ABC绕点A逆时针旋转90°，则在△ABC扫过的区域中（不含边界上的点），到点O的距离为无理数的格点的个数是（ ）