题目内容
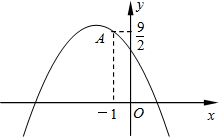 (2012•高淳县一模)如图,已知二次函数y=-
(2012•高淳县一模)如图,已知二次函数y=-| 1 |
| 2 |
| 9 |
| 2 |
(1)求该二次函数的表达式,并写出该函数图象的顶点坐标;
(2)点P(2a,a)(其中a>0),与点Q均在该函数的图象上,且这两点关于图象的对称轴对称,求a的值及点Q到y轴的距离.
分析:(1)把点A的坐标代入二次函数解析式,利用待定系数法求二次函数解析式解答,把函数解析式转化成顶点式解析式,写出顶点坐标即可;
(2)把点P的坐标代入函数解析式计算即可求出a的值,从而得到点P的坐标,再根据二次函数的对称性写出点Q的坐标,然后根据点Q到y轴的距离点Q的纵坐标的绝对值解答.
(2)把点P的坐标代入函数解析式计算即可求出a的值,从而得到点P的坐标,再根据二次函数的对称性写出点Q的坐标,然后根据点Q到y轴的距离点Q的纵坐标的绝对值解答.
解答:解:(1)∵二次函数y=-
x2+mx+3的图象经过点A(-1,
),
∴-
×(-1)2-m+3=
,
解得m=-2,
∴该二次函数的表达式为y=-
x2-2x+3,
∵y=-
x2-2x+3=-
(x+2)2+5,
∴顶点坐标为(-2,5);
(2)∵点P(2a,a)(其中a>0)在该函数图象上,
∴-
×(2a)2-2×2a+3=a,
解得a1=
,a2=-3(舍去),
∴点P的坐标为(1,
),
∵点P、Q关于对称轴x=-2对称,
∴点Q的坐标为(-5,
),
∴点Q到y轴的距离为|-5|=5,
故答案为:a=
,点Q到y轴的距离为5.
| 1 |
| 2 |
| 9 |
| 2 |
∴-
| 1 |
| 2 |
| 9 |
| 2 |
解得m=-2,
∴该二次函数的表达式为y=-
| 1 |
| 2 |
∵y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴顶点坐标为(-2,5);
(2)∵点P(2a,a)(其中a>0)在该函数图象上,
∴-
| 1 |
| 2 |
解得a1=
| 1 |
| 2 |
∴点P的坐标为(1,
| 1 |
| 2 |
∵点P、Q关于对称轴x=-2对称,
∴点Q的坐标为(-5,
| 1 |
| 2 |
∴点Q到y轴的距离为|-5|=5,
故答案为:a=
| 1 |
| 2 |
点评:本题考查了待定系数法求二次函数解析式,二次函数的对称性,以及二次函数图象上点的特征,先求出m的值是解题的关键.

练习册系列答案
相关题目

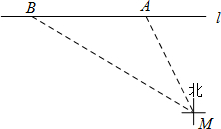 (2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.
(2012•高淳县一模)《中华人民共和国道路交通管理条理》规定:“小汽车在城市街道公路上的行驶速度不得超过70km/h(即19.44m/s)”.如图所示,已知测速站M到街道公路l的距离为90m,一辆小汽车在街道公路l上由东向西行驶,测得此车从点A行驶到点B所用的时间为6s,并测得A在M的北偏西27°方向上,B在M的北偏西60°方向上.求出此车从A到B的平均速度,并判断此车是否超过限速.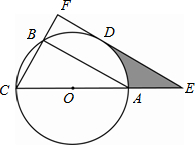 (2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是
(2012•高淳县一模)已知△ABC内接于⊙O,AC是⊙O的直径,D是
 延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.
延长线交于点M,边B1A1与OB交于点N,边B1A1与OA的延长线交于点E,连接MN.