题目内容
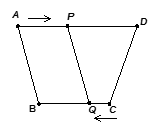
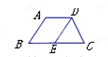
如图，在□ABCD中，CE⊥AB，E为垂足，若AB=4，BC=6，则□ABCD的周长为 ；若∠A=125°，则∠BCE的度数为 ．
 |
20；35°
根据平行四边形的对边相等，即可求出平行四边形的周长；根据平行四边形的对边平行先求出∠B的值，然后利用直角三角形的角的关系，求出∠BCE的度数．
解：∵平行四边形ABCD，
∴AD=BC=6，AB=CD=4，
∴?ABCD的周长=2（4+6）=20；
∵AD∥BC，
∴∠B=180°-∠A=55°，
又∵CE⊥AB，
∴∠BCE=35°．
故答案为：20，35°
解：∵平行四边形ABCD，
∴AD=BC=6，AB=CD=4，
∴?ABCD的周长=2（4+6）=20；
∵AD∥BC，
∴∠B=180°-∠A=55°，
又∵CE⊥AB，
∴∠BCE=35°．
故答案为：20，35°
练习册系列答案
相关题目
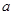cm，其中矩形的长是宽的2倍，那么它们的面积
、
、
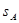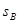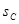之间的关系式正确的是（ ）.
