��Ŀ����
��ͼ��ʾ����ƽ��ֱ������ϵxoy�У�Rt��AOB��ֱ�DZ�OB��OA�ֱ���x���Ϻ�y���ϣ�����OA=2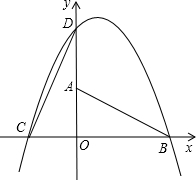 ��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮
��OB=4���ֽ�Rt��AOB����ֱ�Ƕ���O����ʱ�뷽����ת90��õ���COD����֪һ�����߾���C��D��B���㣮��1�������������ߵĽ���ʽ��
��2������DB��P���߶�BC��һ���㣨P����B��C�غϣ�������P��PE��BD��CD��E����DEP������ʱ����PE�Ľ���ʽ��
��3������D���ڴ������߶Գ���ĶԳƵ�F������CF���Գ����ڵ�M����������һ����R��x����һ����Q���������������Ƿ���ڵ�R��x�����Ƿ���ڵ�Q��ʹ����C��M��Q��RΪ������ı�����ƽ���ı��Σ�������ڣ����Q������ꣻ��������ڣ���˵�����ɣ�
��������1��������ת�����ʣ������OC��OD�ij������ɵó�C��D�����꣬�ô���ϵ����������������ߵĽ���ʽ��
��2����E��x��Ĵ��ߣ��费��ΪH�������P�����꣬���ݡ�CPE�ס�CBD�ó��Ķ�Ӧ�ߺͶ�Ӧ�ߵıȣ����EH�ı���ʽ�����ɵó����ڡ�CEP�������P�������ĺ�����ϵʽ���������ú��������ʼ������P��E���꣬�������ô���ϵ�������ֱ��PE�Ľ���ʽ��
��3������Ҫ������������ۣ�����CMΪ�ߣ�����CMΪ�Խ��ߣ��ɸ���ƽ���ı��ε����ʵó�Q��������꣬���������ߵĽ���ʽ�м������Q�����꣮
��2����E��x��Ĵ��ߣ��费��ΪH�������P�����꣬���ݡ�CPE�ס�CBD�ó��Ķ�Ӧ�ߺͶ�Ӧ�ߵıȣ����EH�ı���ʽ�����ɵó����ڡ�CEP�������P�������ĺ�����ϵʽ���������ú��������ʼ������P��E���꣬�������ô���ϵ�������ֱ��PE�Ľ���ʽ��
��3������Ҫ������������ۣ�����CMΪ�ߣ�����CMΪ�Խ��ߣ��ɸ���ƽ���ı��ε����ʵó�Q��������꣬���������ߵĽ���ʽ�м������Q�����꣮
��� �⣺��1���ߡ�COD�ա�AOB
�⣺��1���ߡ�COD�ա�AOB
��OC=OA��OD=OB
��OC=2��OD=4
��C��-2��0��D��0��4��B��4��0��
����������ߵĽ���ʽy=ax2+bx+4��a��0��
��C��-2��O��B��4��0������
��
�������ߵĽ���ʽΪ��y=-
x2+x+4��4�֣�
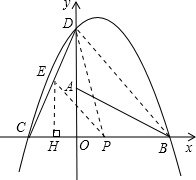 ��2����E��EH��x�ᣬ
��2����E��EH��x�ᣬ
��S��DEP=S��DCP-S��ECP
=
CP•OD-
CP•EH
=
CP��OD-EH��
���P��m��0��
��P��BC֮���˶�
��CP=m+2
��PE��BD
���CEP�ס�CDB
��
=
��
=
��EH=
��S��DEP=
(m+2)(4-
)
=-
(m-1)2+3��6�֣�
�൱m=1ʱ��S��DEP�����ֵΪ3����ʱP��1��0����7�֣�
�֡�D��0��4��
����BD�Ľ���ʽy=kx+4��k��0��
��B��4��0������0=4k+4
k=-1
��BD��y=-x+4
��PE��BD
����PE��y=-x+b��
��P��1��0������
��0=-1+b��
���b=1
��PE�Ľ���ʽΪ��y=-x+1����8�֣�
��3������
��D��0��4��F��2��4��
CF��y=x+2
��M��1��3��
����CM��
��y=-
x2+x+4����y=3
��ã�x1=1+
��x2=1-
��Q1��-2+
��0��Q2��-2-
��0����10�֣�
��y=-3��-
x2+x+4=-3
��ã�x1=1+
��x2=1-
Q3��4+
��0��Q4��4-
��0����12�֣�
����CMΪ�Խ��ߣ�Q5��Q1�غ�
����ĸ���Q��
 �⣺��1���ߡ�COD�ա�AOB
�⣺��1���ߡ�COD�ա�AOB��OC=OA��OD=OB
��OC=2��OD=4
��C��-2��0��D��0��4��B��4��0��
����������ߵĽ���ʽy=ax2+bx+4��a��0��
��C��-2��O��B��4��0������
|
��
|
�������ߵĽ���ʽΪ��y=-
| 1 |
| 2 |
 ��2����E��EH��x�ᣬ
��2����E��EH��x�ᣬ��S��DEP=S��DCP-S��ECP
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
���P��m��0��
��P��BC֮���˶�
��CP=m+2
��PE��BD
���CEP�ס�CDB
��
| EH |
| OD |
| CP |
| BC |
��
| EH |
| 4 |
| m+2 |
| 6 |
��EH=
| 2m+4 |
| 3 |
��S��DEP=
| 1 |
| 2 |
| 2m+4 |
| 3 |
=-
| 1 |
| 3 |
�൱m=1ʱ��S��DEP�����ֵΪ3����ʱP��1��0����7�֣�
�֡�D��0��4��
����BD�Ľ���ʽy=kx+4��k��0��
��B��4��0������0=4k+4
k=-1
��BD��y=-x+4
��PE��BD
����PE��y=-x+b��
��P��1��0������
��0=-1+b��
���b=1
��PE�Ľ���ʽΪ��y=-x+1����8�֣�
��3������
��D��0��4��F��2��4��
CF��y=x+2
��M��1��3��
����CM��
��y=-
| 1 |
| 2 |
��ã�x1=1+
| 3 |
| 3 |
��Q1��-2+
| 3 |
| 3 |
��y=-3��-
| 1 |
| 2 |
��ã�x1=1+
| 15 |
| 15 |
Q3��4+
| 15 |
| 15 |
����CMΪ�Խ��ߣ�Q5��Q1�غ�
����ĸ���Q��
���������⿼���˶��κ�������ʽ��ȷ����ͼ���������ƽ���ı��ε��ж������ʵ�֪ʶ���ۺ���ǿ������Ҫ��ϸߣ�����ѧ���������ۣ����ν�ϵ���ѧ˼�뷽����

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ��
���ڵ�A������A�ֱ���x�ᡢy��Ĵ��ߣ�����Ϊ��B��C������ı���OBAC�������Σ���һ�κ����Ĺ�ϵʽ�� 5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������
5����ͼ��ʾ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ��-2��0���ͣ�2��0�����������Ƶ�B˳ʱ����ת90��õ������ڣ����A�Ķ�Ӧ��A�������Ϊ��������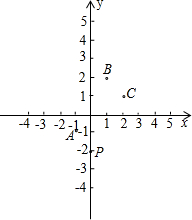 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ��
��ͼ��ʾ����ƽ��ֱ������ϵ�У�һ�����Ӵӵ�P����ʼ���ι��ڵ�A��B��C��ѭ���Գ�����������һ�δӵ�P�������ڵ�A�ĶԳƵ�M�����ڶ��δӵ�M�������ڵ�B�ĶԳƵ�N���������δӵ�N�������ڵ�C�ĶԳƵ㴦���������ȥ�� ��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ
��ͼ��ʾ����ƽ��ֱ������ϵxoy�У���һ��Խ��߳��ֱ�Ϊ1��2��3��������A1B1C1O��A2B2C2B1��A3B3C3B2����Խ���OB1��B1B2��B2 B3���η�����y���ϣ����ڶ����غϣ������������з�ʽ���Խ��߳�Ϊn�ĵ�n�������εĶ���An������Ϊ BE��
BE��