��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OCDE�Ķ���C��E�ֱ���y����������x����������ϣ�OC=8��OE=17��������y=![]() x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
x2��3x+m��y���ཻ�ڵ�A�������ߵĶԳ�����x���ཻ�ڵ�B����CD���ڵ�K��
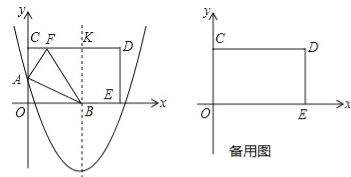
��1��������OCDE��AB�۵�����Oǡ�����ڱ�CD�ϵĵ�F����
����B�������� �� ����BK�ij��� ��CK�ij��� ��
�����F�����ꣻ
����ֱ��д�������ߵĺ�������ʽ��
��2��������OCDE���ž�����E��ֱ���۵�����Oǡ�����ڱ�CD�ϵĵ�G��������OG���ۺ���OG�ཻ�ڵ�H����M���߶�EH�ϵ�һ�����㣨�����H�غϣ�������MG��MO������G��GP��OM�ڵ�P����EH�ڵ�N������ON����M�ӵ�E��ʼ���߶�EH���H�˶��������N�غ�ʱֹͣ����MOG����NOG������ֱ��ʾΪS1��S2���ڵ�M���˶������У�S1S2����S1��S2�Ļ�����ֵ�Ƿ����仯�����仯����ֱ��д���仯��Χ�������䣬��ֱ��д�����ֵ��
��ܰ��ʾ���������Ը������⣬�ڱ���ͼ�в���ͼ�Σ��Ա�����
���𰸡���1����10��0��8��10������4��8������y=![]() x2��3x+5.��2�����䣮S1S2=189��
x2��3x+5.��2�����䣮S1S2=189��
�������������������1���������ı���OCKB�Ǿ����Լ��Գ��ṫʽ���ɽ�����⣮����RT��BKF�����ù��ɶ������ɽ�����⣮����OA=AF=x����RT��ACF�У�AC=8��x��AF=x��CF=4�����ù��ɶ������ɽ�����⣮
��2�����䣮S1S2=189������GHN�ס�MHG����![]() ���õ�GH2=HNHM�����GH2������S1S2=
���õ�GH2=HNHM�����GH2������S1S2=![]() OGHN
OGHN![]() OGHM���ɽ�����⣮
OGHM���ɽ�����⣮
�����������1����ͼ1�У��١�������y=![]() x2��3x+m�ĶԳ���x=��
x2��3x+m�ĶԳ���x=��![]() =10��
=10��
����B���꣨10��0����
���ı���OBKC�Ǿ��Σ�
��CK=OB=10��KB=OC=8��
�ʴ𰸷ֱ�Ϊ10��0��8��10��
����RT��FBK�У��ߡ�FKB=90����BF=OB=10��BK=OC=8��
��FK=![]() =6��
=6��
��CF=CK��FK=4��
����F���꣨4��8����
����OA=AF=x��
��RT��ACF����AC2+CF2=AF2��
����8��x��2+42=x2��
��x=5��
����A���꣨0��5��������������y=![]() x2��3x+m��m=5��
x2��3x+m��m=5��
��������Ϊy=![]() x2��3x+5��
x2��3x+5��
��2�����䣮S1S2=189��
���ɣ���ͼ2�У���RT��EDG�У���GE=EO=17��ED=8��
��DG=![]() =15��
=15��
��CG=CD��DG=2��
��OG=![]() =2
=2![]() ��
��
��CP��OM��MH��OG��
���NPN=��NHG=90����
�ߡ�HNG+��HGN=90������PNM+��PMN=90������HNG=��PNM��
���HGN=��NMP��
�ߡ�NMP=��HMG����GHN=��GHM��
���GHN�ס�MHG��
��![]() ��
��
��GH2=HNHM��
��GH=OH=![]() ��
��
��HNHM=17��
��S1/span>S2=![]() OGHN
OGHN![]() OGHM=��
OGHM=��![]() 2
2![]() ��217=289��
��217=289��


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�