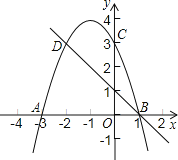
题目内容
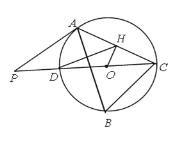
【题目】如图,点C、D在线段AB上,且△PCD是等边三角形.∠APB=120°.
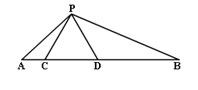
(1)求证:△ACP∽△PDB;
(2)证明:![]()
【答案】(1)见解析 (2)6
【解析】
(1)根据等边三角形的性质得到∠PCD=∠PDC=∠CPD=60°,于是推出∠ACP=∠PDB=120°,等量代换得到∠BPD=∠CAP,根据相似三角形的性质得到结论;
(2)由相似三角形的性质得到![]() ,根据等边三角形的性质得到PC=PD=CD,等量代换得到
,根据等边三角形的性质得到PC=PD=CD,等量代换得到![]() ,即可得到结论.
,即可得到结论.
证明:(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=∠CPD=60°,
∴∠ACP=∠PDB=120°,
∵∠APB=120°,
∴∠APC+∠BPD=60°,
∵∠CAP+∠APC=60°
∴∠BPD=∠CAP,
∴△ACP∽△PDB;
(2)由(1)得△ACP∽△PDB,
∴![]() ,
,
∵△PCD是等边三角形,
∴PC=PD=CD,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目