Question

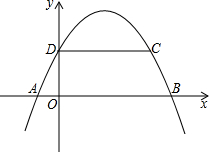如图，抛物线y=ax²-3ax+b经过A（-1，0），C（3，2）两点，与y轴交于点D，与x轴交于另一点B．
（1）求此抛物线的解析式；
（2）若直线y=kx-1（k≠0）将四边形ABCD面积二等分，求k的值．

Answer 1

分析：（1）利用待定系数法，把已知坐标代入解析式求出抛物线解析式．
（2）作辅助线过点C作CH⊥AB于点H，得出四边形ABCD是等腰梯形，由矩形的中心对称性得出过P点且与CD相交的任一直线将梯形ABCD的面积平分．

解答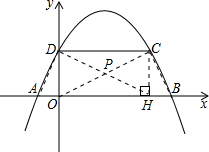：解：（1）∵抛物线y=ax²-3ax+b过A（-1，0）、C（3，2），
∴0=a+3a+b，2=9a-9a+b．
解得a=-

1

2

，b=2，
∴抛物线解析式y=-

1

2

x²+

3

2

x+2．

（2）过点C作CH⊥AB于点H，
由y=-

1

2

x²+

3

2

x+2得B（4，0）、D（0，2）．
∴CD∥AB．
由抛物线的对称性得四边形ABCD是等腰梯形，
∴S_△AOD=S_△BHC．
设矩形ODCH的对称中心为P，则P（

3

2

，1）．
由矩形的中心对称性知：过P点任一直线将它的面积平分．
∴过P点且与CD相交的任一直线将梯形ABCD的面积平分．
当直线y=kx-1经过点P时，
得1=

3

2

k-1
∴k=

4

3

．
∴当k=

4

3

时，直线y=

4

3

x-1将四边形ABCD面积二等分．

点评：此题主要考查了二次函数的综合应用以及平行四边形，梯形的性质，利用数形结合以及中心对称的性质得出是解题关键．