Question

【题目】如图，一座拱桥的轮廓是抛物线型，拱高6，在长度为8的两支柱和之间，还安装着三根支柱，相邻两支柱间的距离为5.

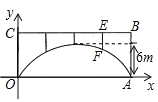
（1）建立如图所示的直角坐标系，求拱桥抛物线的函数表达式；

（2）求支柱的长度.

（3）拱桥下面拟铺设行车道，要保证高3的汽车能够通过（车顶与拱桥的距离不小于0.3），行车道最宽可以铺设多少米？

Answer 1

【答案】（1）；（2）EF=3.5m；（3）行车道最宽可以铺设13.4米.

【解析】

（1）根据题目可知抛物线经过的两点的坐标，设出抛物线的解析式代入可求解；

（2）设N点的坐标为（15，y）可求出支柱EF的长度；

（3）令y=3.3，求得x的值即可求解．

（1）根据题意，设拱桥抛物线的函数表达式为：，

∵相邻两支柱间的距离均为5m，∴OA=4×5m=20m，

∴（20，0），（10，6）两点都在抛物线上，

∴，解得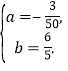

∴．

（2）设点F的坐标为（15，y），

∴．

∴EF=8mm=m=3.5m．

（3）当y=3+0.3=3.3（m）时，有，

化简，得，

解得，，，

∴．

答：行车道最宽可以铺设13.4米．