题目内容
【题目】已知:如图,在△ABC中,∠ABC=45°,AH⊥BC于点H,点D为AH上的一点,且DH=HC,连结BD并延长BD交AC于点E,连结EH.

(1)请补全图形;
(2)直接写出BD与AC的数量关系和位置关系;
(3)求证:∠BEH=45°.
【答案】(1)见解析;(2)BD=AC,BD⊥AC;(3)证明见解析.
【解析】
(1)根据题意直接补全图形;
(2)先判断出△ABH为等腰直角三角形,进而得出△AHC≌△BHD,最后用对顶角和等量代换即可得出∠ADE+∠DAE=90°,结论得证;
(3)先利用同角或等角的余角相等得出结论即可判断出△AHE≌△BHF,即可得出EH=FH,结论得证.
(1)补全图形如图1所示;
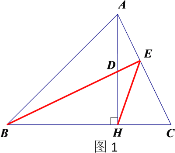
(2)BD=AC ;BD⊥AC;
(3)∵AH⊥BC于点H,∠ABC=45°,
∴△ABH为等腰直角三角形,
∴AH=BH,∠BAH=45°,
在△AHC和△BHD中
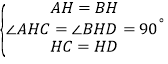 ,
,
∴△AHC≌△BHD,
∴∠1=∠2,
如图2,过点H作HF⊥HE交BE于点F,
∴∠FHE=90°
即∠4+∠5=90°
又∵∠3+∠5=∠AHB=90°
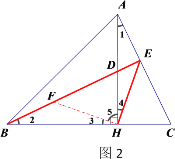
∴∠3=∠4
在△AHE和△BHF中,
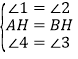
∴△AHE≌△BHF
∴EH=FH
∵∠FHE=90°
∴△FHE是等腰直角三角形
∴∠BEH=45°

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目