Question

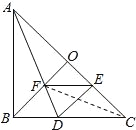
【题目】如图，在Rt△ABC中，AB=CB，BO⊥AC，DA平分∠BAC，DE⊥AC，连接EF，下列结论：①tan∠ADB=2；②图中有4对全等三角形；③若将△DEF沿EF折叠，则点D不一定落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（ ）

A．1个 B．2个 C．3个 D．4个

Answer 1

【答案】C.

【解析】

试题解析：①由折叠可得BD=DE，而DC＞DE，∴DC＞BD，∴tan∠ADB≠2，故①错误；

②图中的全等三角形有△ABF≌△AEF，△ABD≌△AED，△FBD≌△FED，（由折叠可知）

∵OB⊥AC，

∴∠AOB=∠COB=90°，

在Rt△AOB和Rt△COB中，

，

∴Rt△AOB≌Rt△COB（HL），

则全等三角形共有4对，故②正确；

③∵AB=CB，BO⊥AC，把△ABC折叠，

∴∠ABO=∠CBO=45°，∠FBD=∠DEF，

∴∠AEF=∠DEF=45°，∴将△DEF沿EF折叠，可得点D一定在AC上，故③错误；

④∵OB⊥AC，且AB=CB，

∴BO为∠ABC的平分线，即∠ABO=∠OBC=45°，

由折叠可知，AD是∠BAC的平分线，即∠BAF=22.5°，

又∵∠BFD为三角形ABF的外角，

∴∠BFD=∠ABO+∠BAF=67.5°，

易得∠BDF=180°-45°-67.5°=67.5°，

∴∠BFD=∠BDF，

∴BD=BF，故④正确．

⑤连接CF，

∵△AOF和△COF等底同高，

∴S△AOF=S△COF，

∵∠AEF=∠ACD=45°，

∴EF∥CD，

∴S△EFD=S△EFC，

∴S四边形DFOE=S△COF，

∴S四边形DFOE=S△AOF，

故⑤正确；

正确的有3个，

故选C．