题目内容
【题目】如图,∠AOB=90°,反比例函数y=﹣ ![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y= ![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴. 
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y= ![]() 于另一点,求△OBC的面积.
于另一点,求△OBC的面积. 
【答案】
(1)解:∵反比例函数y=﹣ ![]() (x<0)的图象过点A(﹣1,a),
(x<0)的图象过点A(﹣1,a),
∴a=﹣ ![]() =2,
=2,
∴A(﹣1,2),
过A作AE⊥x轴于E,BF⊥⊥x轴于F,
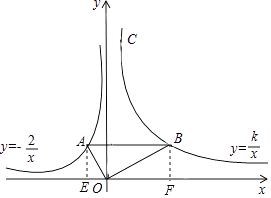
∴AE=2,OE=1,
∵AB∥x轴,
∴BF=2,
∵∠AOB=90°,
∴∠EAO+∠AOE=∠AOE+∠BOF=90°,
∴∠EAO=∠BOF,
∴△AEO∽△OFB,
∴ ![]() ,
,
∴OF=4,
∴B(4,2),
∴k=4×2=8;
(2)解:∵直线OA过A(﹣1,2),
∴直线AO的解析式为y=﹣2x,
∵MN∥OA,
∴设直线MN的解析式为y=﹣2x+b,
∴2=﹣2×4+b,
∴b=10,
∴直线MN的解析式为y=﹣2x+10,
∵直线MN交x轴于点M,交y轴于点N,
∴M(5,0),N(0,10),
解 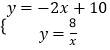 得,
得, ![]() 或
或 ![]() ,
,
∴C(1,8),
∴△OBC的面积=S△OMN﹣S△OCN﹣S△OBM= ![]() 5×10﹣
5×10﹣ ![]() ×10×1﹣
×10×1﹣ ![]() ×5×2=15.
×5×2=15.
【解析】(1)把A(﹣1,a)代入反比例函数y=﹣ ![]() 得到A(﹣1,2),过A作AE⊥x轴于E,BF⊥⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;(2)求的直线AO的解析式为y=﹣2x,设直线MN的解析式为y=﹣2x+b,得到直线MN的解析式为y=﹣2x+10,解方程组得到C(1,8),于是得到结论.
得到A(﹣1,2),过A作AE⊥x轴于E,BF⊥⊥x轴于F,根据相似三角形的性质得到B(4,2),于是得到k=4×2=8;(2)求的直线AO的解析式为y=﹣2x,设直线MN的解析式为y=﹣2x+b,得到直线MN的解析式为y=﹣2x+10,解方程组得到C(1,8),于是得到结论.
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案