��Ŀ����
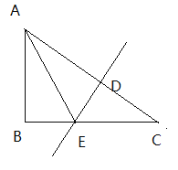
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪԭ�㣬ƽ���ı���ABCD�ı�BC��x���ϣ�D����y���ϣ�C������Ϊ��2��0����BC=6����BCD=60�㣬��E��AB��һ�㣬AE=3EB����P��D��O��C���㣬������y=ax2+bx+c����D��B��C���㣮
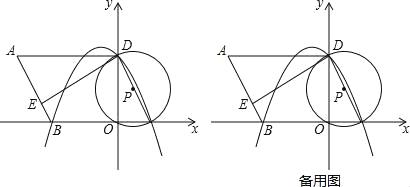
��1����ֱ��д����B��D�����꣺B�� ����D�� ����
��2���������ߵĽ���ʽ��
��3����֤��ED����P�����ߣ�
��4������MΪ�����ߵĶ��㣬��ֱ��д��ƽ���ϵ�N�����꣬ʹ���Ե�B��D��M��NΪ������ı���Ϊƽ���ı��Σ�
���𰸡���1����-4��0����D��0��2![]() ������2��y=-
������2��y=-![]() x2-
x2-![]() x+
x+![]() ��(3)֤������������4����N������Ϊ��-5��
��(3)֤������������4����N������Ϊ��-5��![]() ������3��
������3��![]() ������-3��-
������-3��-![]() ����
����
��������
�����������1����ȷ��B��-4��0��������Rt��OCD��������OCD���������OD=2![]() ���ɵ�D��0��2
���ɵ�D��0��2![]() ����
����
��2�����ý���ʽ������ϵ�������������ߵĽ���ʽ��
��3���ȼ����CD=2OC=4���ٸ���ƽ���ı��ε����ʣ�������������ε��ж��ɵ���AED�ס�COD���������������ε����ʺ�Բ�ܽǶ����õ�CDΪ��P��ֱ�������Ǹ������ߵ��ж������õ�ED����P�����ߣ�
��4�������䷽�õ�y=-![]() ��x+1��2+
��x+1��2+![]() ������ƽ���ı��ε����ʺ͵�ƽ�ƵĹ��ɣ����÷������۵ķ���ȷ��N�����꣮
������ƽ���ı��ε����ʺ͵�ƽ�ƵĹ��ɣ����÷������۵ķ���ȷ��N�����꣮
�����������1����C��2��0����BC=6��
��B��-4��0����
��Rt��OCD����tan��OCD=![]() ��
��
��OD=2tan60��=![]() ��
��
��D��0��![]() ����
����
��2���������ߵĽ���ʽΪy=a��x+4����x-2����
��D��0��![]() �������a��4����-2��=
�������a��4����-2��=![]() �����a=-
�����a=-![]() ��
��
�������ߵĽ���ʽΪy=-![]() ��x+4����x-2��=-
��x+4����x-2��=-![]() x2-
x2-![]() x+
x+![]() ��
��
��3����Rt��OCD��CD=2OC=4��
���ı���ABCDΪƽ���ı��Σ�
��AB=CD=4��AB��CD����A=��BCD=60�㣬AD=BC=6��
��AE=3BE��
��AE=3��
��![]() ,
,![]() ��
��
��![]() ��
��
�ߡ�DAE=��DCB��
���AED�ס�COD��
���ADE=��CDO��
�ߡ�ADE+��ODE=90��
���CDO+��ODE=90�㣬
��CD��DE��
�ߡ�DOC=90�㣬
��CDΪ��P��ֱ����
��ED����P�����ߣ�
��4�����ڣ�
��y=-![]() x2-
x2-![]() x+
x+![]() =-
=-![]() ��x+1��2+
��x+1��2+![]() ��
��
��M��-1��![]() ����
����
��B��-4��0����D��0��![]() ����
����
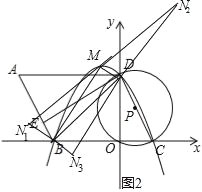
��ͼ2��
��BMΪƽ���ı���BDMN�ĶԽ���ʱ����D����ƽ��4����λ��������ƽ��![]() ����λ�õ���B�����M��-1��
����λ�õ���B�����M��-1��![]() ������ƽ��4����λ��������ƽ��
������ƽ��4����λ��������ƽ��![]() ����λ�õ���N1��-5��
����λ�õ���N1��-5��![]() ����
����
��DMΪƽ���ı���BDMN�ĶԽ���ʱ����B����ƽ��3����λ��������ƽ��![]() ����λ�õ���M�����D��0��
����λ�õ���M�����D��0��![]() ������ƽ��3����λ��������ƽ��
������ƽ��3����λ��������ƽ��![]() ����λ�õ���N2��3��
����λ�õ���N2��3��![]() ����
����
��BDΪƽ���ı���BDMN�ĶԽ���ʱ����M����ƽ��3����λ��������ƽ��![]() ����λ�õ���B�����D��0��
����λ�õ���B�����D��0��![]() ������ƽ��3����λ��������ƽ��
������ƽ��3����λ��������ƽ��![]() ����λ�õ���N3��-3��-
����λ�õ���N3��-3��-![]() ����
����
������������N��������-5��![]() ������3��
������3��![]() ������-3��-
������-3��-![]() ����
����

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�