Question

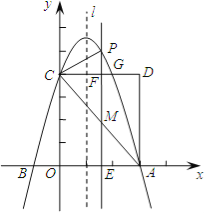
【题目】请阅读以下材料，并完成相应的任务：

任务：

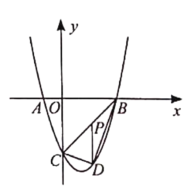
（1）设P（a，），R（b，），求直线OM的函数解析式（用含a，b的代数式表示），并说明Q点在直线OM上；

（2）证明：∠MOB=∠AOB．

Answer 1

【答案】（1），说明见解析；（2）见解析

【解析】

（1）根据题意，得M（b，），再进一步运用待定系数法求解；根据题意，得Q（a，），代入求得的直线解析式说明Q点在直线OM上；

（2）连接PR，交OM于点S，结合矩形的性质、等腰三角形的性质和三角形的外角的性质即可证明；

（1）解：设直线OM的函数表达式为y=kx，

由题意可得四边形PQRM为矩形，且P（a，），R（b，），

∴M（b，），Q（a，）

把点M（b，）代入y=kx得k=

∴直线OM的函数表达式为

∵Q的坐标（a，）满足，

∴点Q在直线OM上．

（2）证明：连接PR，交OM于点S

由题意得四边形PQRM是矩形，

∴PR=QM

而SP=PR，SM=QM，

∴SP= SM

∴∠1=∠2．

∴∠3=∠1+∠2=2∠2

∵PR=2PO，

∴PS=PO．

∴∠4=∠3=2∠2．

∵PM∥x轴

∴∠2=∠5．

∴∠AOB=∠4+∠5=3∠5．

即∠MOB=∠AOB