��Ŀ����
��ͼ���ھ���ABCD�У�AB=4��AD=2����P��Qͬʱ�ӵ�A��������P��ÿ��2����λ���ٶ���ABCD�ķ����˶�����Q��ÿ��1����λ���ٶ���ADC�ķ����˶�����P��Q��������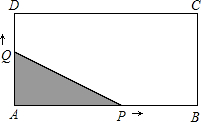 ʱ������ͬʱֹͣ�˶�����P��Q�����˶���ʱ��Ϊx���룩����APQ�����ΪS��ƽ����λ����
ʱ������ͬʱֹͣ�˶�����P��Q�����˶���ʱ��Ϊx���룩����APQ�����ΪS��ƽ����λ����
��1����P��Q�ӳ������������õ�ʱ����
��2����S��x֮��ĺ�����ϵʽ��
��3����S=
ʱ����x��ֵ��
 ʱ������ͬʱֹͣ�˶�����P��Q�����˶���ʱ��Ϊx���룩����APQ�����ΪS��ƽ����λ����
ʱ������ͬʱֹͣ�˶�����P��Q�����˶���ʱ��Ϊx���룩����APQ�����ΪS��ƽ����λ������1����P��Q�ӳ������������õ�ʱ����
4
4
�룻��2����S��x֮��ĺ�����ϵʽ��
��3����S=
| 7 | 2 |
��������1������������ʱ������ʻ��·��Ϊ4��2+2��2=12��������·�̡��ٶ�=ʱ�䣬���м��㼴�ɣ�
��2����0��x��2ʱ��P����AB�ϣ�Q����AD�ϣ�����������������м��㼴�ɣ�
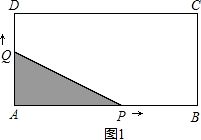
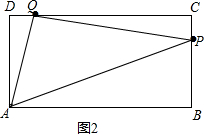
��2��x��3ʱ��P����CB�ϣ�PB=2x-4��CP=6-x��Q����CD�ϣ�DQ=x-2��QC=6-2x���ó�����ABCD�����-������ADQ�����-������QCP�����-������ABP������ɵ�������QAP���������3��x��4ʱ����QP=4-DQ-CP=12-3x��������������������м��㼴�ɣ�
��3����S=
���루2���еĽ���ʽ�������x��ֵ��
��2����0��x��2ʱ��P����AB�ϣ�Q����AD�ϣ�����������������м��㼴�ɣ�
��2��x��3ʱ��P����CB�ϣ�PB=2x-4��CP=6-x��Q����CD�ϣ�DQ=x-2��QC=6-2x���ó�����ABCD�����-������ADQ�����-������QCP�����-������ABP������ɵ�������QAP���������3��x��4ʱ����QP=4-DQ-CP=12-3x��������������������м��㼴�ɣ�
��3����S=
| 7 |
| 2 |
���
 �⣺��1����4��2+2��2���£�2+1��=4��
�⣺��1����4��2+2��2���£�2+1��=4��
�ʴ�Ϊ��4��
��2����ͼ1����0��x��2ʱ��S=
AQ��AP=
•x•2x=x2��
��ͼ2����2��x��3ʱ��
�ɳ�����ABCD�����-S��ADQ-S��QCP-S��ABP=S��QAP
=4��2-
��2����x-2��-
��4����2x-4��-
����6-x������6-2x��
=-x2+4x��
��ͼ3����3��x��4ʱ��S=
��AD��QP=
��2����12-3x��=12-3x��

��3����0��x��2ʱ��x2=
����ã�x=��
��
��x=
��
��2��x��3ʱ��-x2+4x=
����ã�x=2��
����x=2+
��
��3��x��4ʱ��12-3x=
����ã�x=
��С��3����ȥ�����ʴ�ʱ�����ڣ�

 �⣺��1����4��2+2��2���£�2+1��=4��
�⣺��1����4��2+2��2���£�2+1��=4���ʴ�Ϊ��4��
��2����ͼ1����0��x��2ʱ��S=
| 1 |
| 2 |
| 1 |
| 2 |
��ͼ2����2��x��3ʱ��
�ɳ�����ABCD�����-S��ADQ-S��QCP-S��ABP=S��QAP
=4��2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=-x2+4x��
��ͼ3����3��x��4ʱ��S=
| 1 |
| 2 |
| 1 |
| 2 |

��3����0��x��2ʱ��x2=
| 7 |
| 2 |
| ||
| 2 |
��x=
| ||
| 2 |
��2��x��3ʱ��-x2+4x=
| 7 |
| 2 |
| ||
| 2 |
| ||
| 2 |
��3��x��4ʱ��12-3x=
| 7 |
| 2 |
| 17 |
| 6 |
������������Ҫ�����˶��κ����������ε�������㣬�Լ�һԪ���η��̵ļ��㣬�ؼ��Ǹ���x��ȡֵ��Χ��ʾ��S��x֮��ĺ�����ϵʽ��

��ϰ��ϵ�д�
�����Ŀ
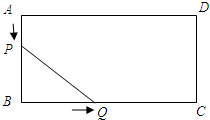 ��ͼ���ھ���ABCD�У�AB=4cm��BC=8cm����P�ӵ�A������1cm/s���ٶ����B�˶�����Q�ӵ�B������2cm/s���ٶ����C�˶����辭����ʱ��Ϊxs����PBQ�����Ϊycm2��������ͼ���ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������
��ͼ���ھ���ABCD�У�AB=4cm��BC=8cm����P�ӵ�A������1cm/s���ٶ����B�˶�����Q�ӵ�B������2cm/s���ٶ����C�˶����辭����ʱ��Ϊxs����PBQ�����Ϊycm2��������ͼ���ܷ�ӳy��x֮��ĺ�����ϵ���ǣ�������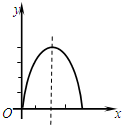
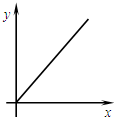
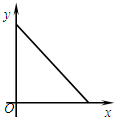
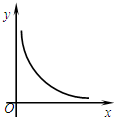
 ��
��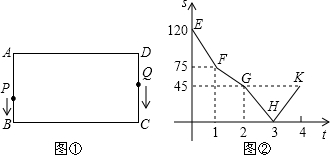 �������У�Q��ͣ����1s��ͼ����P��Q����������AB-BC-CD������·��S��cm����ʱ��t��s��֮��ĺ�����ϵͼ��
�������У�Q��ͣ����1s��ͼ����P��Q����������AB-BC-CD������·��S��cm����ʱ��t��s��֮��ĺ�����ϵͼ��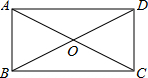 ��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB=60�㣬AB=6����AD=��������
��ͼ���ھ���ABCD�У��Խ���AC��BD�ཻ�ڵ�O����AOB=60�㣬AB=6����AD=��������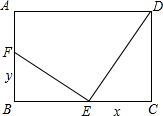 DE��EF��AB���ڵ�F����CE=x��BF=y��
DE��EF��AB���ڵ�F����CE=x��BF=y��